题目
(x)=dfrac (1)(3)(x)^3-(x)^2-8x+1的单调增加区间是( )(x)=dfrac (1)(3)(x)^3-(x)^2-8x+1(x)=dfrac (1)(3)(x)^3-(x)^2-8x+1(x)=dfrac (1)(3)(x)^3-(x)^2-8x+1(x)=dfrac (1)(3)(x)^3-(x)^2-8x+1
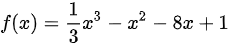 的单调增加区间是( )
的单调增加区间是( )
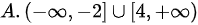
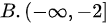
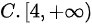
题目解答
答案
本题考查函数的单调性,因为
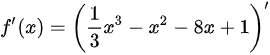
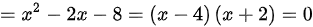 ,
,
因此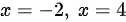 .
.
当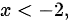
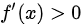 ,函数单调增加,
,函数单调增加,
当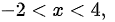
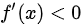 ,函数单调减少,
,函数单调减少,
当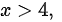
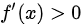 ,函数单调增加,
,函数单调增加,
又因为函数在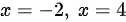 处连续,故
处连续,故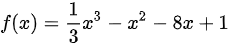 的单调增加区间是
的单调增加区间是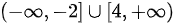 ,因此本题选择A.
,因此本题选择A.
解析
考查要点:本题主要考查利用导数确定函数的单调区间,属于导数应用的基础题型。
解题思路:
- 求导:先对函数$f(x)$求导,得到$f'(x)$。
- 求临界点:解方程$f'(x)=0$,找到导数为零的点,即函数的临界点。
- 划分区间:根据临界点将定义域划分为若干区间。
- 判断符号:在每个区间内取测试点,判断导数的符号,从而确定函数的单调性。
- 确定区间端点:注意导数为零的点是否包含在单调区间内。
关键点:
- 导数的正负决定单调性:导数为正时函数递增,导数为负时函数递减。
- 临界点的包含性:若导数在临界点两侧符号改变,则该点属于相邻的单调区间。
步骤1:求导数
函数$f(x)=\dfrac{1}{3}x^3 -x^2 -8x +1$的导数为:
$f'(x) = x^2 - 2x -8.$
步骤2:求导数的零点
解方程$f'(x)=0$:
$x^2 - 2x -8 = 0 \implies (x-4)(x+2) = 0,$
解得$x = 4$和$x = -2$。
步骤3:划分区间并判断导数符号
临界点将数轴分为三个区间:
- 当$x < -2$时,取测试点$x=-3$,代入$f'(x)$得:
$f'(-3) = (-3)^2 - 2(-3) -8 = 9 +6 -8 = 7 > 0,$
因此函数在$(-\infty, -2)$上单调递增。 - 当$-2 < x < 4$时,取测试点$x=0$,代入$f'(x)$得:
$f'(0) = 0^2 - 2 \cdot 0 -8 = -8 < 0,$
因此函数在$(-2, 4)$上单调递减。 - 当$x > 4$时,取测试点$x=5$,代入$f'(x)$得:
$f'(5) = 5^2 - 2 \cdot 5 -8 = 25 -10 -8 = 7 > 0,$
因此函数在$(4, +\infty)$上单调递增。
步骤4:确定单调区间端点
- 在$x=-2$处,导数由正变负,函数在此处达到极大值,因此$x=-2$属于递增区间。
- 在$x=4$处,导数由负变正,函数在此处达到极小值,因此$x=4$属于递增区间。
综上,函数$f(x)$的单调递增区间为$(-\infty, -2] \cup [4, +\infty)$。