题目
(3)lim-1+tanx -√1+sinx
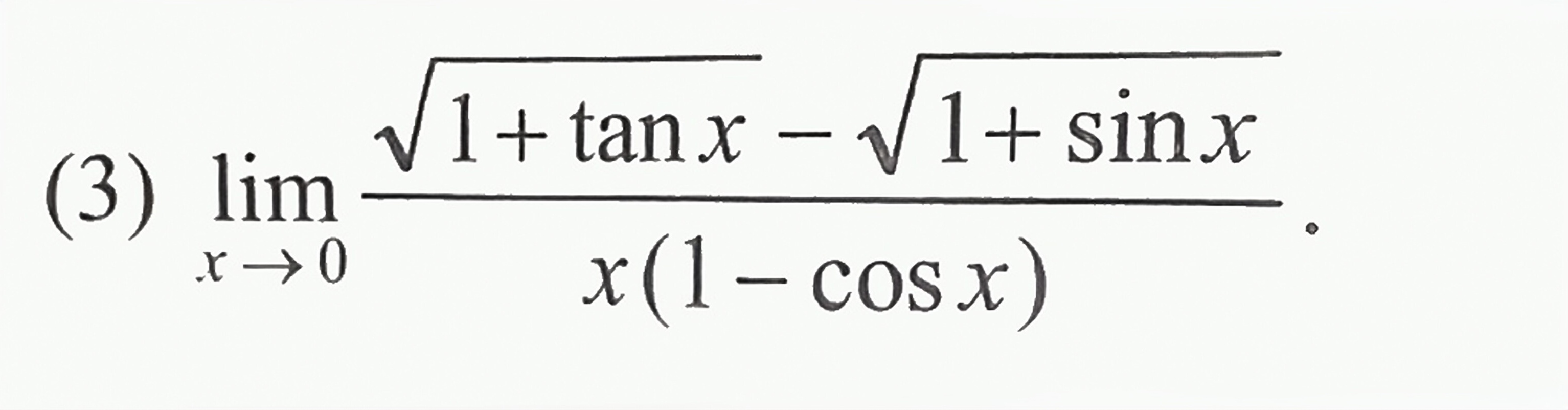
题目解答
答案
本题考查了极限的求法,
$\lim _{x\rightarrow 0}\dfrac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x(1-\cos x)}$
$=\lim _{x\rightarrow 0}\dfrac{1+\tan x-1-\sin x}{x(1-\cos x)(\sqrt{1+\tan x}+\sqrt{1+\sin x})}$
$=\lim _{x\rightarrow 0}\dfrac{\tan x-\sin x}{x(1-\cos x)(\sqrt{1+\tan x}+\sqrt{1+\sin x})}$
$=\lim _{x\rightarrow 0}\dfrac{\tan x(1-\cos x)}{x(1-\cos x)(\sqrt{1+\tan x}+\sqrt{1+\sin x})}$
$=\lim _{x\rightarrow 0}\dfrac{1}{(\sqrt{1+\tan x}+\sqrt{1+\sin x})}$
$=\dfrac{1}{2}$
$\dfrac{1}{2}$
$\lim _{x\rightarrow 0}\dfrac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x(1-\cos x)}$
$=\lim _{x\rightarrow 0}\dfrac{1+\tan x-1-\sin x}{x(1-\cos x)(\sqrt{1+\tan x}+\sqrt{1+\sin x})}$
$=\lim _{x\rightarrow 0}\dfrac{\tan x-\sin x}{x(1-\cos x)(\sqrt{1+\tan x}+\sqrt{1+\sin x})}$
$=\lim _{x\rightarrow 0}\dfrac{\tan x(1-\cos x)}{x(1-\cos x)(\sqrt{1+\tan x}+\sqrt{1+\sin x})}$
$=\lim _{x\rightarrow 0}\dfrac{1}{(\sqrt{1+\tan x}+\sqrt{1+\sin x})}$
$=\dfrac{1}{2}$
$\dfrac{1}{2}$
解析
步骤 1:化简表达式
首先,我们注意到题目中的表达式是 $\lim _{x\rightarrow 0}\dfrac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x(1-\cos x)}$。为了简化这个表达式,我们可以通过乘以共轭表达式来消除根号。具体来说,我们乘以 $\dfrac{\sqrt{1+\tan x}+\sqrt{1+\sin x}}{\sqrt{1+\tan x}+\sqrt{1+\sin x}}$,这样分子就变成了 $(1+\tan x)-(1+\sin x)$,即 $\tan x-\sin x$。
步骤 2:进一步化简
接下来,我们注意到 $\tan x-\sin x$ 可以写成 $\sin x(\frac{1}{\cos x}-1)$,即 $\sin x(\frac{1-\cos x}{\cos x})$。因此,原表达式可以写成 $\lim _{x\rightarrow 0}\dfrac{\sin x(1-\cos x)}{x(1-\cos x)(\sqrt{1+\tan x}+\sqrt{1+\sin x})\cos x}$。
步骤 3:计算极限
由于 $\lim _{x\rightarrow 0}\dfrac{\sin x}{x}=1$,$\lim _{x\rightarrow 0}\cos x=1$,以及 $\lim _{x\rightarrow 0}\sqrt{1+\tan x}=\sqrt{1+0}=1$ 和 $\lim _{x\rightarrow 0}\sqrt{1+\sin x}=\sqrt{1+0}=1$,我们可以得出 $\lim _{x\rightarrow 0}\dfrac{1}{(\sqrt{1+\tan x}+\sqrt{1+\sin x})}=\dfrac{1}{2}$。
首先,我们注意到题目中的表达式是 $\lim _{x\rightarrow 0}\dfrac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x(1-\cos x)}$。为了简化这个表达式,我们可以通过乘以共轭表达式来消除根号。具体来说,我们乘以 $\dfrac{\sqrt{1+\tan x}+\sqrt{1+\sin x}}{\sqrt{1+\tan x}+\sqrt{1+\sin x}}$,这样分子就变成了 $(1+\tan x)-(1+\sin x)$,即 $\tan x-\sin x$。
步骤 2:进一步化简
接下来,我们注意到 $\tan x-\sin x$ 可以写成 $\sin x(\frac{1}{\cos x}-1)$,即 $\sin x(\frac{1-\cos x}{\cos x})$。因此,原表达式可以写成 $\lim _{x\rightarrow 0}\dfrac{\sin x(1-\cos x)}{x(1-\cos x)(\sqrt{1+\tan x}+\sqrt{1+\sin x})\cos x}$。
步骤 3:计算极限
由于 $\lim _{x\rightarrow 0}\dfrac{\sin x}{x}=1$,$\lim _{x\rightarrow 0}\cos x=1$,以及 $\lim _{x\rightarrow 0}\sqrt{1+\tan x}=\sqrt{1+0}=1$ 和 $\lim _{x\rightarrow 0}\sqrt{1+\sin x}=\sqrt{1+0}=1$,我们可以得出 $\lim _{x\rightarrow 0}\dfrac{1}{(\sqrt{1+\tan x}+\sqrt{1+\sin x})}=\dfrac{1}{2}$。