题目

证明方程^5-3x=1至少有一个根介于 1 和 2 之间

证明方程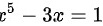 $x^5-3x=1$ 至少有一个根介于 1 和 2 之间

题目解答

答案

解：

方程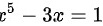 $x^5-3x=1$ 至少有一个根介于 1 和 2 之间，等价于 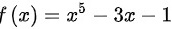$f\left(x\right)=x^5-3x-1$ 至少有一个零点于 1 和 2 之间

$f\left(1\right)=-3;\ f\left(2\right)=25;\$

$f\left(1\right)f\left(2\right)=-3\times25=-75<0$

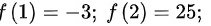
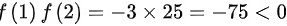
根据零点定理，至少有一个零点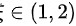 $\xi\in\left(1,2\right)$

故方程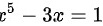 $x^5-3x=1$ 至少有一个根介于 1 和 2 之间

解析

步骤 1：定义函数
定义函数$f(x)={x}^{5}-3x-1$，这样原方程${x}^{5}-3x=1$可以转化为$f(x)=0$的形式，即寻找函数$f(x)$的零点。
步骤 2：计算$f(1)$和$f(2)$
计算$f(1)$和$f(2)$的值，以确定函数在区间$[1,2]$的端点处的符号。
步骤 3：应用零点定理
根据零点定理，如果函数$f(x)$在区间$[a,b]$上连续，且$f(a)$和$f(b)$异号，那么在$(a,b)$内至少存在一个零点。