题目
若函数 y = y ( x ) 在区间 (0,+infty ) 内是微分方程初值问(0,+infty )的特解则 y ( x ) 的最大 值 _
若函数 y = y ( x ) 在区间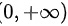 
内是微分方程初值问
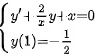的特解则 y ( x ) 的最大 值 _
题目解答
答案
∵
∴
∴
∴
∴
∴
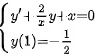
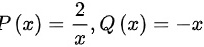
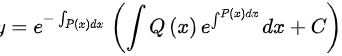
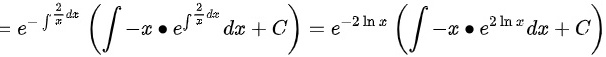
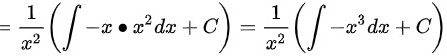
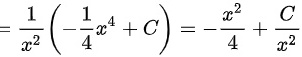
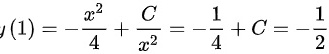
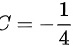
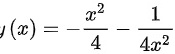
∴y ( x ) 的最大值是0
解析
步骤 1：求解微分方程
给定的微分方程是 $y' + \frac{2}{x}y + x = 0$。这是一个一阶线性微分方程，可以使用积分因子法求解。首先，我们找到积分因子 $e^{\int \frac{2}{x} dx}$，即 $e^{2\ln x} = x^2$。然后，将原方程两边同时乘以积分因子 $x^2$，得到 $x^2y' + 2xy + x^3 = 0$。这可以写成 $(x^2y)' = -x^3$。接下来，对两边积分，得到 $x^2y = -\frac{1}{4}x^4 + C$，其中 $C$ 是积分常数。因此，$y = -\frac{1}{4}x^2 + \frac{C}{x^2}$。
步骤 2：确定积分常数
根据初始条件 $y(1) = -\frac{1}{2}$，代入 $y = -\frac{1}{4}x^2 + \frac{C}{x^2}$，得到 $-\frac{1}{2} = -\frac{1}{4} + C$。解得 $C = -\frac{1}{4}$。因此，$y = -\frac{1}{4}x^2 - \frac{1}{4x^2}$。
步骤 3：求解最大值
为了找到 $y(x)$ 的最大值，我们需要求导并找到导数为零的点。$y' = -\frac{1}{2}x + \frac{1}{2x^3}$。令 $y' = 0$，得到 $-\frac{1}{2}x + \frac{1}{2x^3} = 0$，即 $x^4 = 1$。在区间 $(0, +\infty)$ 内，$x = 1$。将 $x = 1$ 代入 $y$，得到 $y(1) = -\frac{1}{4} - \frac{1}{4} = -\frac{1}{2}$。因此，$y(x)$ 的最大值是 $-\frac{1}{2}$。
给定的微分方程是 $y' + \frac{2}{x}y + x = 0$。这是一个一阶线性微分方程，可以使用积分因子法求解。首先，我们找到积分因子 $e^{\int \frac{2}{x} dx}$，即 $e^{2\ln x} = x^2$。然后，将原方程两边同时乘以积分因子 $x^2$，得到 $x^2y' + 2xy + x^3 = 0$。这可以写成 $(x^2y)' = -x^3$。接下来，对两边积分，得到 $x^2y = -\frac{1}{4}x^4 + C$，其中 $C$ 是积分常数。因此，$y = -\frac{1}{4}x^2 + \frac{C}{x^2}$。
步骤 2：确定积分常数
根据初始条件 $y(1) = -\frac{1}{2}$，代入 $y = -\frac{1}{4}x^2 + \frac{C}{x^2}$，得到 $-\frac{1}{2} = -\frac{1}{4} + C$。解得 $C = -\frac{1}{4}$。因此，$y = -\frac{1}{4}x^2 - \frac{1}{4x^2}$。
步骤 3：求解最大值
为了找到 $y(x)$ 的最大值，我们需要求导并找到导数为零的点。$y' = -\frac{1}{2}x + \frac{1}{2x^3}$。令 $y' = 0$，得到 $-\frac{1}{2}x + \frac{1}{2x^3} = 0$，即 $x^4 = 1$。在区间 $(0, +\infty)$ 内，$x = 1$。将 $x = 1$ 代入 $y$，得到 $y(1) = -\frac{1}{4} - \frac{1}{4} = -\frac{1}{2}$。因此，$y(x)$ 的最大值是 $-\frac{1}{2}$。