题目
求(int )_(-1)^1xln (1+(e)^x)dx.
求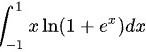 .
.
题目解答
答案
根据奇偶函数定积分的性质,得:
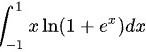
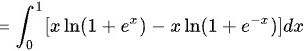
合并,得:
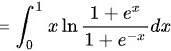
化简,得:
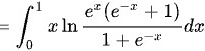
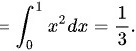
解析
步骤 1:利用奇偶函数的性质
观察被积函数$f(x)=x\ln(1+e^x)$,发现$f(-x)=-x\ln(1+e^{-x})$,因此$f(x)$是一个奇函数。根据奇函数在对称区间上的积分性质,即$\int_{-a}^{a}f(x)dx=0$,如果$f(x)$是奇函数,我们可以将原积分拆分为两部分,利用奇函数的性质简化计算。
步骤 2:拆分积分
将原积分拆分为两部分,即${\int }_{-1}^{1}x\ln (1+{e}^{x})dx={\int }_{-1}^{0}x\ln (1+{e}^{x})dx+{\int }_{0}^{1}x\ln (1+{e}^{x})dx$。由于$f(x)$是奇函数,${\int }_{-1}^{0}x\ln (1+{e}^{x})dx$和${\int }_{0}^{1}x\ln (1+{e}^{x})dx$在数值上相等但符号相反,因此它们的和为0。但是,为了更清晰地展示计算过程,我们继续进行变形。
步骤 3:变形与化简
将${\int }_{-1}^{1}x\ln (1+{e}^{x})dx$变形为${\int }_{0}^{1}x\ln \dfrac {1+{e}^{x}}{1+{e}^{-x}}dx$,这是因为奇函数的性质使得${\int }_{-1}^{0}x\ln (1+{e}^{x})dx$与${\int }_{0}^{1}x\ln (1+{e}^{-x})dx$在数值上相等但符号相反,因此可以合并为${\int }_{0}^{1}x\ln \dfrac {1+{e}^{x}}{1+{e}^{-x}}dx$。进一步化简,得到${\int }_{0}^{1}x\ln \dfrac {{e}^{x}({e}^{-x}+1)}{1+{e}^{-x}}dx$,即${\int }_{0}^{1}x\ln {e}^{x}dx$,简化为${\int }_{0}^{1}x^2dx$。
步骤 4:计算积分
计算${\int }_{0}^{1}x^2dx$,得到$\dfrac{1}{3}x^3|_{0}^{1}=\dfrac{1}{3}$。
观察被积函数$f(x)=x\ln(1+e^x)$,发现$f(-x)=-x\ln(1+e^{-x})$,因此$f(x)$是一个奇函数。根据奇函数在对称区间上的积分性质,即$\int_{-a}^{a}f(x)dx=0$,如果$f(x)$是奇函数,我们可以将原积分拆分为两部分,利用奇函数的性质简化计算。
步骤 2:拆分积分
将原积分拆分为两部分,即${\int }_{-1}^{1}x\ln (1+{e}^{x})dx={\int }_{-1}^{0}x\ln (1+{e}^{x})dx+{\int }_{0}^{1}x\ln (1+{e}^{x})dx$。由于$f(x)$是奇函数,${\int }_{-1}^{0}x\ln (1+{e}^{x})dx$和${\int }_{0}^{1}x\ln (1+{e}^{x})dx$在数值上相等但符号相反,因此它们的和为0。但是,为了更清晰地展示计算过程,我们继续进行变形。
步骤 3:变形与化简
将${\int }_{-1}^{1}x\ln (1+{e}^{x})dx$变形为${\int }_{0}^{1}x\ln \dfrac {1+{e}^{x}}{1+{e}^{-x}}dx$,这是因为奇函数的性质使得${\int }_{-1}^{0}x\ln (1+{e}^{x})dx$与${\int }_{0}^{1}x\ln (1+{e}^{-x})dx$在数值上相等但符号相反,因此可以合并为${\int }_{0}^{1}x\ln \dfrac {1+{e}^{x}}{1+{e}^{-x}}dx$。进一步化简,得到${\int }_{0}^{1}x\ln \dfrac {{e}^{x}({e}^{-x}+1)}{1+{e}^{-x}}dx$,即${\int }_{0}^{1}x\ln {e}^{x}dx$,简化为${\int }_{0}^{1}x^2dx$。
步骤 4:计算积分
计算${\int }_{0}^{1}x^2dx$,得到$\dfrac{1}{3}x^3|_{0}^{1}=\dfrac{1}{3}$。