题目
lim _(xarrow 0)((1-x))^dfrac (1{2x)}=( ).
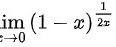 =( ).
=( ).
题目解答
答案
进行简单的取对数计算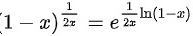
显然有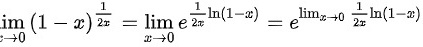
进行简单的取极限计算会发现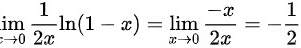
那么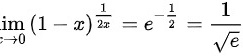
故本题答案为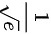 .
.
解析
步骤 1:取对数
将原式${(1-x)}^{\dfrac {1}{2x}}$写成指数形式,即${(1-x)}^{\dfrac {1}{2x}}={e}^{\dfrac {1}{2x}\ln (1-x)}$。
步骤 2:求极限
求极限$\lim _{x\rightarrow 0}{e}^{\dfrac {1}{2x}\ln (1-x)}$,首先求$\lim _{x\rightarrow 0}\dfrac {1}{2x}\ln (1-x)$。
步骤 3:洛必达法则
由于$\lim _{x\rightarrow 0}\dfrac {1}{2x}\ln (1-x)$是$\dfrac{0}{0}$型不定式,使用洛必达法则,即$\lim _{x\rightarrow 0}\dfrac {\ln (1-x)}{2x}=\lim _{x\rightarrow 0}\dfrac {\dfrac {d}{dx}[\ln (1-x)]}{\dfrac {d}{dx}[2x]}=\lim _{x\rightarrow 0}\dfrac {-\dfrac {1}{1-x}}{2}=-\dfrac {1}{2}$。
步骤 4:计算最终结果
将$\lim _{x\rightarrow 0}\dfrac {1}{2x}\ln (1-x)=-\dfrac {1}{2}$代入${e}^{\dfrac {1}{2x}\ln (1-x)}$,得到$\lim _{x\rightarrow 0}{(1-x)}^{\dfrac {1}{2x}}={e}^{-\dfrac {1}{2}}=\dfrac {1}{\sqrt {e}}$。
将原式${(1-x)}^{\dfrac {1}{2x}}$写成指数形式,即${(1-x)}^{\dfrac {1}{2x}}={e}^{\dfrac {1}{2x}\ln (1-x)}$。
步骤 2:求极限
求极限$\lim _{x\rightarrow 0}{e}^{\dfrac {1}{2x}\ln (1-x)}$,首先求$\lim _{x\rightarrow 0}\dfrac {1}{2x}\ln (1-x)$。
步骤 3:洛必达法则
由于$\lim _{x\rightarrow 0}\dfrac {1}{2x}\ln (1-x)$是$\dfrac{0}{0}$型不定式,使用洛必达法则,即$\lim _{x\rightarrow 0}\dfrac {\ln (1-x)}{2x}=\lim _{x\rightarrow 0}\dfrac {\dfrac {d}{dx}[\ln (1-x)]}{\dfrac {d}{dx}[2x]}=\lim _{x\rightarrow 0}\dfrac {-\dfrac {1}{1-x}}{2}=-\dfrac {1}{2}$。
步骤 4:计算最终结果
将$\lim _{x\rightarrow 0}\dfrac {1}{2x}\ln (1-x)=-\dfrac {1}{2}$代入${e}^{\dfrac {1}{2x}\ln (1-x)}$,得到$\lim _{x\rightarrow 0}{(1-x)}^{\dfrac {1}{2x}}={e}^{-\dfrac {1}{2}}=\dfrac {1}{\sqrt {e}}$。