题目
(4) int (e)^x(sin )^2xdx.
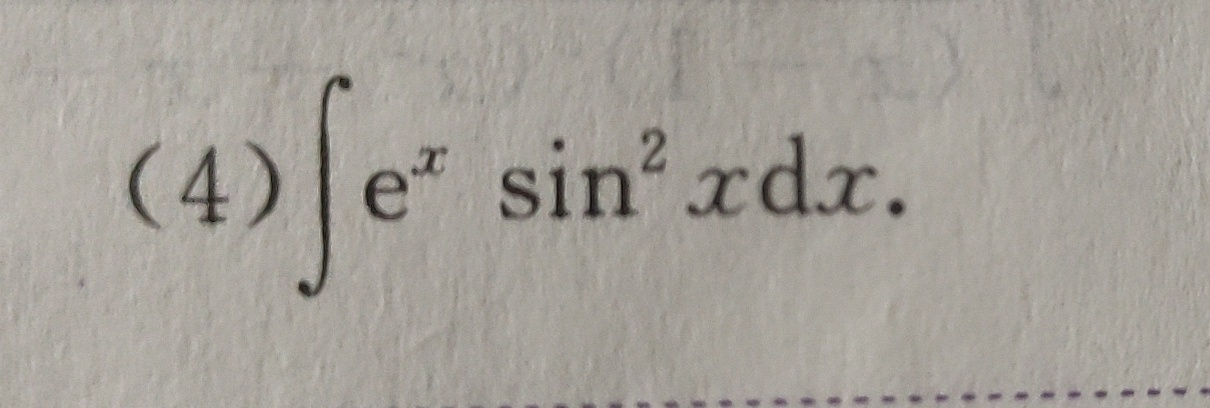
题目解答
答案

解析
步骤 1:使用三角恒等式
首先,我们使用三角恒等式 ${\sin }^{2}x = \frac{1 - \cos 2x}{2}$ 将原积分转换为更易于处理的形式。
步骤 2:积分转换
将 ${\sin }^{2}x$ 替换为 $\frac{1 - \cos 2x}{2}$,得到 $\int {e}^{x} \frac{1 - \cos 2x}{2} dx$。
步骤 3:分配积分
将积分分配为两个独立的积分:$\frac{1}{2} \int {e}^{x} dx - \frac{1}{2} \int {e}^{x} \cos 2x dx$。
步骤 4:计算第一个积分
计算 $\frac{1}{2} \int {e}^{x} dx$,得到 $\frac{1}{2} {e}^{x}$。
步骤 5:使用分部积分法计算第二个积分
对于 $\frac{1}{2} \int {e}^{x} \cos 2x dx$,我们使用分部积分法。设 $u = \cos 2x$,$dv = {e}^{x} dx$,则 $du = -2\sin 2x dx$,$v = {e}^{x}$。根据分部积分公式 $\int u dv = uv - \int v du$,我们得到 $\frac{1}{2} {e}^{x} \cos 2x + \int {e}^{x} \sin 2x dx$。
步骤 6:再次使用分部积分法
对于 $\int {e}^{x} \sin 2x dx$,我们再次使用分部积分法。设 $u = \sin 2x$,$dv = {e}^{x} dx$,则 $du = 2\cos 2x dx$,$v = {e}^{x}$。根据分部积分公式,我们得到 ${e}^{x} \sin 2x - 2 \int {e}^{x} \cos 2x dx$。
步骤 7:合并结果
将步骤 4 和步骤 6 的结果合并,得到 $\frac{1}{2} {e}^{x} - \frac{1}{2} {e}^{x} \cos 2x - \int {e}^{x} \cos 2x dx$。
步骤 8:解方程
将步骤 7 的结果与步骤 5 的结果合并,得到 $\frac{1}{2} {e}^{x} - \frac{1}{2} {e}^{x} \cos 2x - \frac{1}{2} {e}^{x} \cos 2x - \int {e}^{x} \cos 2x dx = \frac{1}{2} {e}^{x} - {e}^{x} \cos 2x - \int {e}^{x} \cos 2x dx$。将 $\int {e}^{x} \cos 2x dx$ 移到等式左边,得到 $\frac{3}{2} \int {e}^{x} \cos 2x dx = \frac{1}{2} {e}^{x} - {e}^{x} \cos 2x$。解方程得到 $\int {e}^{x} \cos 2x dx = \frac{{e}^{x} - 2{e}^{x} \cos 2x}{3}$。
步骤 9:合并最终结果
将步骤 4 和步骤 8 的结果合并,得到 $\frac{1}{2} {e}^{x} - \frac{1}{2} \frac{{e}^{x} - 2{e}^{x} \cos 2x}{3} = \frac{{e}^{x} \sin 2x - 2\cos 2x{e}^{x}}{5}$。
首先,我们使用三角恒等式 ${\sin }^{2}x = \frac{1 - \cos 2x}{2}$ 将原积分转换为更易于处理的形式。
步骤 2:积分转换
将 ${\sin }^{2}x$ 替换为 $\frac{1 - \cos 2x}{2}$,得到 $\int {e}^{x} \frac{1 - \cos 2x}{2} dx$。
步骤 3:分配积分
将积分分配为两个独立的积分:$\frac{1}{2} \int {e}^{x} dx - \frac{1}{2} \int {e}^{x} \cos 2x dx$。
步骤 4:计算第一个积分
计算 $\frac{1}{2} \int {e}^{x} dx$,得到 $\frac{1}{2} {e}^{x}$。
步骤 5:使用分部积分法计算第二个积分
对于 $\frac{1}{2} \int {e}^{x} \cos 2x dx$,我们使用分部积分法。设 $u = \cos 2x$,$dv = {e}^{x} dx$,则 $du = -2\sin 2x dx$,$v = {e}^{x}$。根据分部积分公式 $\int u dv = uv - \int v du$,我们得到 $\frac{1}{2} {e}^{x} \cos 2x + \int {e}^{x} \sin 2x dx$。
步骤 6:再次使用分部积分法
对于 $\int {e}^{x} \sin 2x dx$,我们再次使用分部积分法。设 $u = \sin 2x$,$dv = {e}^{x} dx$,则 $du = 2\cos 2x dx$,$v = {e}^{x}$。根据分部积分公式,我们得到 ${e}^{x} \sin 2x - 2 \int {e}^{x} \cos 2x dx$。
步骤 7:合并结果
将步骤 4 和步骤 6 的结果合并,得到 $\frac{1}{2} {e}^{x} - \frac{1}{2} {e}^{x} \cos 2x - \int {e}^{x} \cos 2x dx$。
步骤 8:解方程
将步骤 7 的结果与步骤 5 的结果合并,得到 $\frac{1}{2} {e}^{x} - \frac{1}{2} {e}^{x} \cos 2x - \frac{1}{2} {e}^{x} \cos 2x - \int {e}^{x} \cos 2x dx = \frac{1}{2} {e}^{x} - {e}^{x} \cos 2x - \int {e}^{x} \cos 2x dx$。将 $\int {e}^{x} \cos 2x dx$ 移到等式左边,得到 $\frac{3}{2} \int {e}^{x} \cos 2x dx = \frac{1}{2} {e}^{x} - {e}^{x} \cos 2x$。解方程得到 $\int {e}^{x} \cos 2x dx = \frac{{e}^{x} - 2{e}^{x} \cos 2x}{3}$。
步骤 9:合并最终结果
将步骤 4 和步骤 8 的结果合并,得到 $\frac{1}{2} {e}^{x} - \frac{1}{2} \frac{{e}^{x} - 2{e}^{x} \cos 2x}{3} = \frac{{e}^{x} \sin 2x - 2\cos 2x{e}^{x}}{5}$。