题目
[题目]若 lim _(xarrow infty )(dfrac ({x)^2+1}(x+1)-ax-b)=0, 求a,b的值.
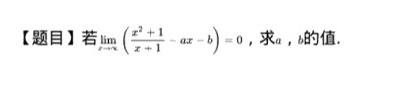
题目解答
答案
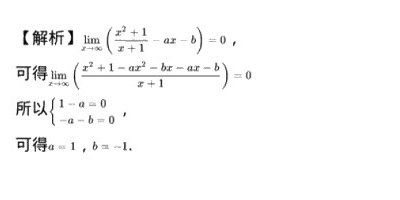
解析
步骤 1:化简表达式
首先,我们化简给定的表达式 $\dfrac {{x}^{2}+1}{x+1}-ax-b$。为了方便处理,我们先将分子进行因式分解或展开,以便于后续的极限计算。
$$\dfrac {{x}^{2}+1}{x+1}-ax-b = \dfrac{x^2+1-ax(x+1)-b(x+1)}{x+1}$$
$$= \dfrac{x^2+1-ax^2-ax-bx-b}{x+1}$$
$$= \dfrac{(1-a)x^2-(a+b)x+(1-b)}{x+1}$$
步骤 2:分析极限条件
根据题目条件,当 $x\rightarrow \infty$ 时,上述表达式的极限为0。这意味着分子的最高次项系数必须为0,否则极限不会为0。因此,我们有:
$$1-a=0$$
解得:
$$a=1$$
步骤 3:求解b的值
将 $a=1$ 代入分子,得到:
$$\dfrac{(1-1)x^2-(1+b)x+(1-b)}{x+1} = \dfrac{-(1+b)x+(1-b)}{x+1}$$
为了使极限为0,分子的线性项系数也必须为0,即:
$$-(1+b)=0$$
解得:
$$b=-1$$
首先,我们化简给定的表达式 $\dfrac {{x}^{2}+1}{x+1}-ax-b$。为了方便处理,我们先将分子进行因式分解或展开,以便于后续的极限计算。
$$\dfrac {{x}^{2}+1}{x+1}-ax-b = \dfrac{x^2+1-ax(x+1)-b(x+1)}{x+1}$$
$$= \dfrac{x^2+1-ax^2-ax-bx-b}{x+1}$$
$$= \dfrac{(1-a)x^2-(a+b)x+(1-b)}{x+1}$$
步骤 2:分析极限条件
根据题目条件,当 $x\rightarrow \infty$ 时,上述表达式的极限为0。这意味着分子的最高次项系数必须为0,否则极限不会为0。因此,我们有:
$$1-a=0$$
解得:
$$a=1$$
步骤 3:求解b的值
将 $a=1$ 代入分子,得到:
$$\dfrac{(1-1)x^2-(1+b)x+(1-b)}{x+1} = \dfrac{-(1+b)x+(1-b)}{x+1}$$
为了使极限为0,分子的线性项系数也必须为0,即:
$$-(1+b)=0$$
解得:
$$b=-1$$