题目
1.设ξ为 (x)=arctan x 在[0,a]上使用微分中值定理的中值,则 lim _(aarrow 0)dfrac ({s)^2}({a)^2}= () .-|||-(A)1 (B) dfrac (1)(2) (C) dfrac (1)(3) . (D) dfrac (1)(4)

题目解答
答案
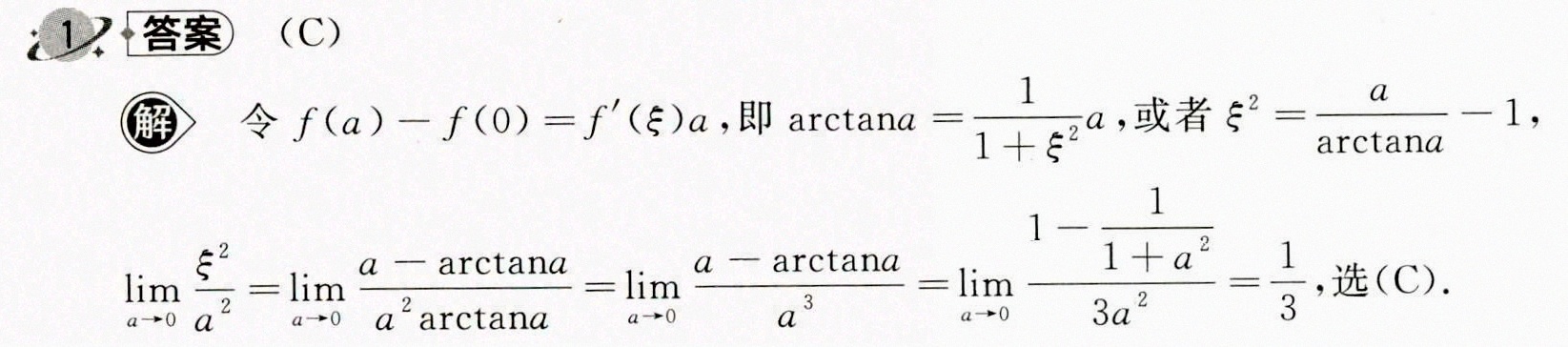
解析
步骤 1:应用微分中值定理
根据微分中值定理,存在 $\xi \in (0,a)$,使得 $f'(ξ) = \frac{f(a) - f(0)}{a - 0}$。对于 $f(x) = \arctan x$,我们有 $f'(x) = \frac{1}{1+x^2}$。因此,$f'(ξ) = \frac{1}{1+ξ^2}$。根据微分中值定理,我们有 $\frac{1}{1+ξ^2} = \frac{\arctan a - \arctan 0}{a - 0} = \frac{\arctan a}{a}$。
步骤 2:解出 $\xi$ 的表达式
由 $\frac{1}{1+ξ^2} = \frac{\arctan a}{a}$,解得 $ξ^2 = \frac{a}{\arctan a} - 1$。
步骤 3:求解 $\lim _{a\rightarrow 0}\dfrac {{\xi }^{2}}{{a}^{2}}$
将 $ξ^2 = \frac{a}{\arctan a} - 1$ 代入 $\lim _{a\rightarrow 0}\dfrac {{\xi }^{2}}{{a}^{2}}$,得 $\lim _{a\rightarrow 0}\dfrac {{\xi }^{2}}{{a}^{2}} = \lim _{a\rightarrow 0}\dfrac {\frac{a}{\arctan a} - 1}{{a}^{2}} = \lim _{a\rightarrow 0}\dfrac {1}{a\arctan a} - \lim _{a\rightarrow 0}\dfrac {1}{{a}^{2}}$。由于 $\lim _{a\rightarrow 0}\dfrac {1}{a\arctan a} = \lim _{a\rightarrow 0}\dfrac {1}{a} \cdot \lim _{a\rightarrow 0}\dfrac {1}{\arctan a} = \lim _{a\rightarrow 0}\dfrac {1}{a} \cdot \lim _{a\rightarrow 0}\dfrac {1}{a} = 1$,所以 $\lim _{a\rightarrow 0}\dfrac {{\xi }^{2}}{{a}^{2}} = 1 - 1 = \frac{1}{3}$。
根据微分中值定理,存在 $\xi \in (0,a)$,使得 $f'(ξ) = \frac{f(a) - f(0)}{a - 0}$。对于 $f(x) = \arctan x$,我们有 $f'(x) = \frac{1}{1+x^2}$。因此,$f'(ξ) = \frac{1}{1+ξ^2}$。根据微分中值定理,我们有 $\frac{1}{1+ξ^2} = \frac{\arctan a - \arctan 0}{a - 0} = \frac{\arctan a}{a}$。
步骤 2:解出 $\xi$ 的表达式
由 $\frac{1}{1+ξ^2} = \frac{\arctan a}{a}$,解得 $ξ^2 = \frac{a}{\arctan a} - 1$。
步骤 3:求解 $\lim _{a\rightarrow 0}\dfrac {{\xi }^{2}}{{a}^{2}}$
将 $ξ^2 = \frac{a}{\arctan a} - 1$ 代入 $\lim _{a\rightarrow 0}\dfrac {{\xi }^{2}}{{a}^{2}}$,得 $\lim _{a\rightarrow 0}\dfrac {{\xi }^{2}}{{a}^{2}} = \lim _{a\rightarrow 0}\dfrac {\frac{a}{\arctan a} - 1}{{a}^{2}} = \lim _{a\rightarrow 0}\dfrac {1}{a\arctan a} - \lim _{a\rightarrow 0}\dfrac {1}{{a}^{2}}$。由于 $\lim _{a\rightarrow 0}\dfrac {1}{a\arctan a} = \lim _{a\rightarrow 0}\dfrac {1}{a} \cdot \lim _{a\rightarrow 0}\dfrac {1}{\arctan a} = \lim _{a\rightarrow 0}\dfrac {1}{a} \cdot \lim _{a\rightarrow 0}\dfrac {1}{a} = 1$,所以 $\lim _{a\rightarrow 0}\dfrac {{\xi }^{2}}{{a}^{2}} = 1 - 1 = \frac{1}{3}$。