题目
讨论函数 (x)=lim _(narrow infty )dfrac (1-{x)^2n}(1+{x)^2n}x的连续性. 若有间断点, 判断其类型.
讨论函数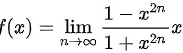 
的连续性. 若有间断点, 判断其类型.
题目解答
答案
解：根据原式化简成分段函数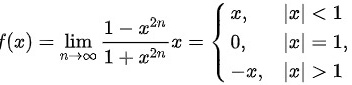
，显然,函数在
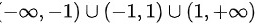上连续.而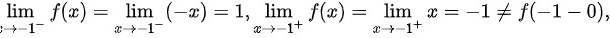
故 x=-1 是 f(x) 的第一类的跳跃间断点.
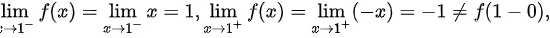故 x=1 也是 f(x) 的第一类的跳跃间断点.
解析
步骤 1：化简函数
首先，我们化简函数 $f(x)=\lim _{n\rightarrow \infty }\dfrac {1-{x}^{2n}}{1+{x}^{2n}}x$。根据 $x^{2n}$ 的性质，当 $|x|<1$ 时，$x^{2n}$ 趋向于 0；当 $|x|=1$ 时，$x^{2n}$ 等于 1；当 $|x|>1$ 时，$x^{2n}$ 趋向于无穷大。因此，我们可以将函数化简为分段函数。
步骤 2：分段函数
根据上述分析，我们可以将函数 $f(x)$ 化简为分段函数 $f(x)=\left \{ \begin{matrix} x,|x|\lt 1\\ 0,|x|=1,\\ -x,|x|\gt 1\end{matrix} \right.$。
步骤 3：判断连续性
根据分段函数的定义，函数在 $(-\infty ,-1)\cup (-1,1)\cup (1,+\infty )$ 上连续。接下来，我们判断 $x=-1$ 和 $x=1$ 处的连续性。
步骤 4：判断 $x=-1$ 处的连续性
计算 $\lim _{x\rightarrow {1}^{-}}f(x)=\lim _{x\rightarrow {1}^{-}}(-x)=1$ 和 $\lim _{x\rightarrow {1}^{-}}f(x)=\lim _{x\rightarrow {1}^{-}}x=-1\neq f(-1-0)$，因此 $x=-1$ 是 $f(x)$ 的第一类的跳跃间断点。
步骤 5：判断 $x=1$ 处的连续性
计算 $\lim _{x\rightarrow {1}^{-}}f(x)=\lim _{x\rightarrow {1}^{-}}x=1$ 和 $\lim _{x\rightarrow {1}^{+}}f(x)=\lim _{x\rightarrow {1}^{-}}(-x)=-1\neq f(1-0)$，因此 $x=1$ 也是 $f(x)$ 的第一类的跳跃间断点。
首先，我们化简函数 $f(x)=\lim _{n\rightarrow \infty }\dfrac {1-{x}^{2n}}{1+{x}^{2n}}x$。根据 $x^{2n}$ 的性质，当 $|x|<1$ 时，$x^{2n}$ 趋向于 0；当 $|x|=1$ 时，$x^{2n}$ 等于 1；当 $|x|>1$ 时，$x^{2n}$ 趋向于无穷大。因此，我们可以将函数化简为分段函数。
步骤 2：分段函数
根据上述分析，我们可以将函数 $f(x)$ 化简为分段函数 $f(x)=\left \{ \begin{matrix} x,|x|\lt 1\\ 0,|x|=1,\\ -x,|x|\gt 1\end{matrix} \right.$。
步骤 3：判断连续性
根据分段函数的定义，函数在 $(-\infty ,-1)\cup (-1,1)\cup (1,+\infty )$ 上连续。接下来，我们判断 $x=-1$ 和 $x=1$ 处的连续性。
步骤 4：判断 $x=-1$ 处的连续性
计算 $\lim _{x\rightarrow {1}^{-}}f(x)=\lim _{x\rightarrow {1}^{-}}(-x)=1$ 和 $\lim _{x\rightarrow {1}^{-}}f(x)=\lim _{x\rightarrow {1}^{-}}x=-1\neq f(-1-0)$，因此 $x=-1$ 是 $f(x)$ 的第一类的跳跃间断点。
步骤 5：判断 $x=1$ 处的连续性
计算 $\lim _{x\rightarrow {1}^{-}}f(x)=\lim _{x\rightarrow {1}^{-}}x=1$ 和 $\lim _{x\rightarrow {1}^{+}}f(x)=\lim _{x\rightarrow {1}^{-}}(-x)=-1\neq f(1-0)$，因此 $x=1$ 也是 $f(x)$ 的第一类的跳跃间断点。