题目
1、已知 f(x)= ) ax+2,xgt 0 (e)^x+1,xleqslant 0 . 在 x=0 处可导,则 a= __ a
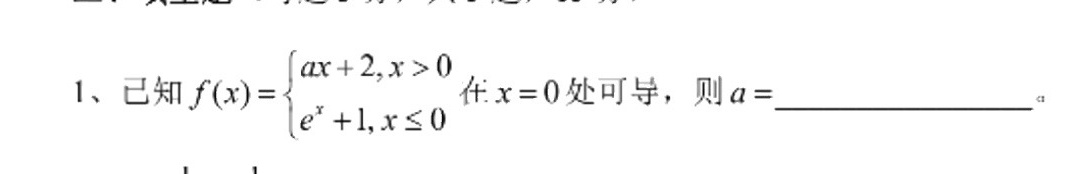
题目解答
答案

解析
步骤 1:确定函数在 x=0 处的连续性
函数在 x=0 处可导,首先需要在 x=0 处连续。因此,需要满足:
$$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^-} f(x) = f(0)$$
步骤 2:计算左右极限
对于 x > 0,函数为 f(x) = ax + 2,因此:
$$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} (ax + 2) = 2$$
对于 x ≤ 0,函数为 f(x) = e^x + 1,因此:
$$\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} (e^x + 1) = e^0 + 1 = 2$$
步骤 3:确定函数在 x=0 处的导数
函数在 x=0 处可导,需要满足:
$$\lim_{x \to 0^+} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^-} \frac{f(x) - f(0)}{x - 0}$$
对于 x > 0,函数为 f(x) = ax + 2,因此:
$$\lim_{x \to 0^+} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^+} \frac{ax + 2 - 2}{x} = \lim_{x \to 0^+} a = a$$
对于 x ≤ 0,函数为 f(x) = e^x + 1,因此:
$$\lim_{x \to 0^-} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^-} \frac{e^x + 1 - 2}{x} = \lim_{x \to 0^-} \frac{e^x - 1}{x} = \lim_{x \to 0^-} \frac{e^x}{1} = 1$$
步骤 4:求解 a
根据步骤 3,可得:
$$a = 1$$
函数在 x=0 处可导,首先需要在 x=0 处连续。因此,需要满足:
$$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^-} f(x) = f(0)$$
步骤 2:计算左右极限
对于 x > 0,函数为 f(x) = ax + 2,因此:
$$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} (ax + 2) = 2$$
对于 x ≤ 0,函数为 f(x) = e^x + 1,因此:
$$\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} (e^x + 1) = e^0 + 1 = 2$$
步骤 3:确定函数在 x=0 处的导数
函数在 x=0 处可导,需要满足:
$$\lim_{x \to 0^+} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^-} \frac{f(x) - f(0)}{x - 0}$$
对于 x > 0,函数为 f(x) = ax + 2,因此:
$$\lim_{x \to 0^+} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^+} \frac{ax + 2 - 2}{x} = \lim_{x \to 0^+} a = a$$
对于 x ≤ 0,函数为 f(x) = e^x + 1,因此:
$$\lim_{x \to 0^-} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^-} \frac{e^x + 1 - 2}{x} = \lim_{x \to 0^-} \frac{e^x - 1}{x} = \lim_{x \to 0^-} \frac{e^x}{1} = 1$$
步骤 4:求解 a
根据步骤 3,可得:
$$a = 1$$