题目
14)/ lim _(xarrow 0)dfrac (x)(f(3x))=2, 则 lim _(xarrow 0)dfrac (f(2x))(x) 的值为 () 。(2014电商、电-|||-(A) dfrac (1)(6); (B) 1/2; (C) dfrac (4)(3); (D) 1/3。
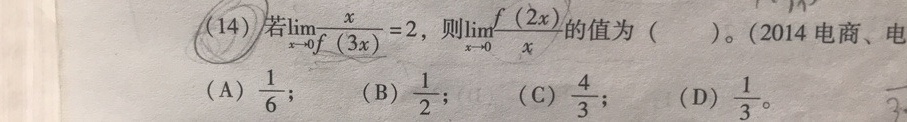
题目解答
答案
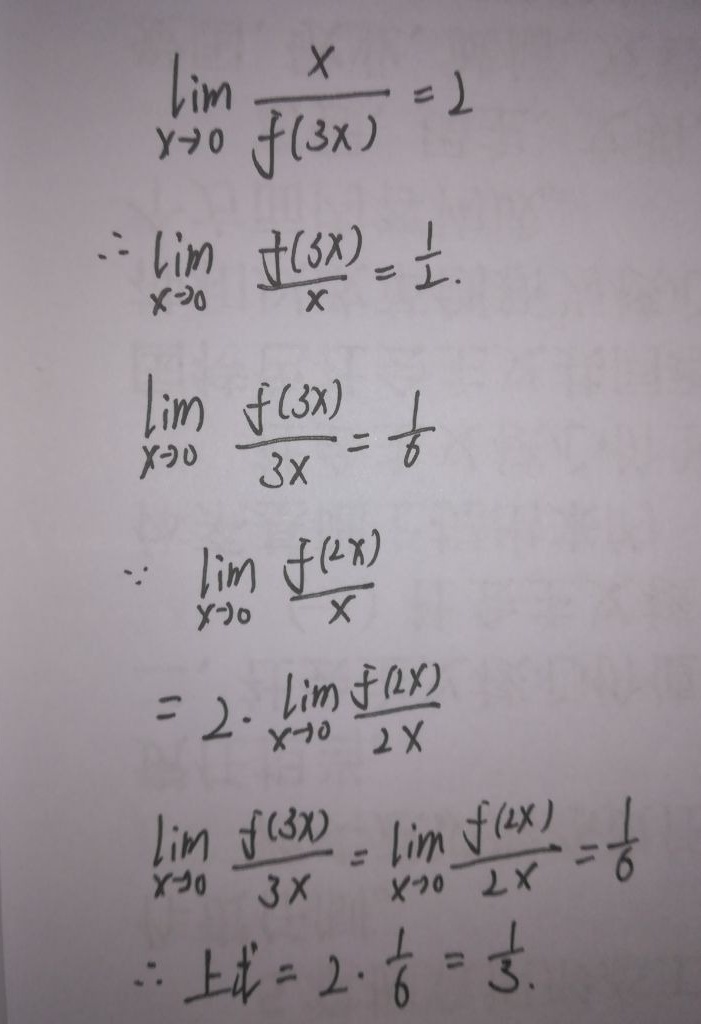
解析
步骤 1:利用已知条件求解 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{x}$
已知 $\lim _{x\rightarrow 0}\dfrac {x}{f(3x)}=2$,则 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{x}=\dfrac {1}{2}$。
步骤 2:求解 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{3x}$
由于 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{x}=\dfrac {1}{2}$,则 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{3x}=\dfrac {1}{6}$。
步骤 3:求解 $\lim _{x\rightarrow 0}\dfrac {f(2x)}{x}$
由于 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{3x}=\lim _{x\rightarrow 0}\dfrac {f(2x)}{2x}=\dfrac {1}{6}$,则 $\lim _{x\rightarrow 0}\dfrac {f(2x)}{x}=2\cdot \dfrac {1}{6}=\dfrac {1}{3}$。
已知 $\lim _{x\rightarrow 0}\dfrac {x}{f(3x)}=2$,则 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{x}=\dfrac {1}{2}$。
步骤 2:求解 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{3x}$
由于 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{x}=\dfrac {1}{2}$,则 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{3x}=\dfrac {1}{6}$。
步骤 3:求解 $\lim _{x\rightarrow 0}\dfrac {f(2x)}{x}$
由于 $\lim _{x\rightarrow 0}\dfrac {f(3x)}{3x}=\lim _{x\rightarrow 0}\dfrac {f(2x)}{2x}=\dfrac {1}{6}$,则 $\lim _{x\rightarrow 0}\dfrac {f(2x)}{x}=2\cdot \dfrac {1}{6}=\dfrac {1}{3}$。