题目
int dfrac ({(1-x))^2}(x(1+{x)^2)}dx
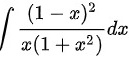
题目解答
答案
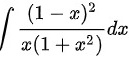
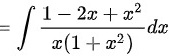
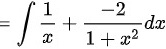
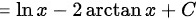
解析
步骤 1:展开分子
将分子 $(1-x)^2$ 展开为 $1 - 2x + x^2$。
步骤 2:分解被积函数
将被积函数 $\dfrac{1 - 2x + x^2}{x(1+x^2)}$ 分解为 $\dfrac{1}{x} + \dfrac{-2}{1+x^2}$。
步骤 3:积分
对分解后的函数进行积分,得到 $\ln x - 2\arctan x + C$。
将分子 $(1-x)^2$ 展开为 $1 - 2x + x^2$。
步骤 2:分解被积函数
将被积函数 $\dfrac{1 - 2x + x^2}{x(1+x^2)}$ 分解为 $\dfrac{1}{x} + \dfrac{-2}{1+x^2}$。
步骤 3:积分
对分解后的函数进行积分,得到 $\ln x - 2\arctan x + C$。