求下列极限:(1)lim _(xarrow 1)dfrac ({x)^2+x-2}({x)^2-3x+2};(2)lim _(xarrow 1)dfrac ({x)^2+x-2}({x)^2-3x+2};(3)lim _(xarrow 1)dfrac ({x)^2+x-2}({x)^2-3x+2};(4)lim _(xarrow 1)dfrac ({x)^2+x-2}({x)^2-3x+2};(5)lim _(xarrow 1)dfrac ({x)^2+x-2}({x)^2-3x+2}
求下列极限:
(1)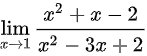 ;
;
(2)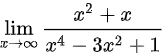 ;
;
(3)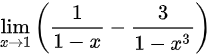 ;
;
(4)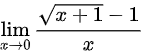 ;
;
(5)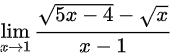
题目解答
答案
(1)极限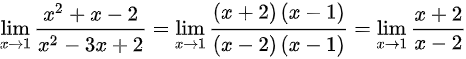
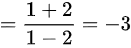 ;
;
(2)使分子分母同时提出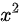 ,我们知
,我们知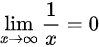 ,
,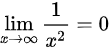 ,得到极限
,得到极限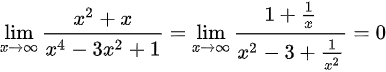 ;
;
(3)极限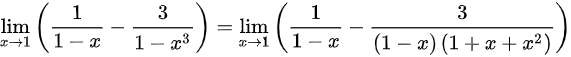
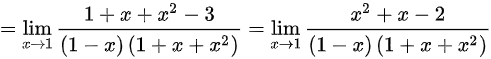
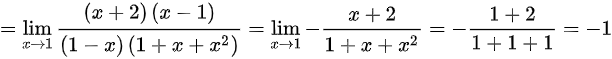 ;
;
(4)由等价无穷小可知,当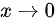 时,满足
时,满足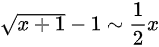 ,故极限
,故极限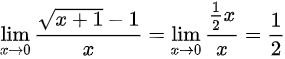 ;
;
(5)对于极限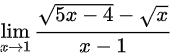 ,其为
,其为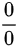 型未定式,利用洛必达法则,故极限为
型未定式,利用洛必达法则,故极限为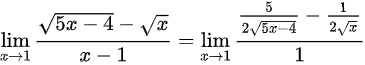
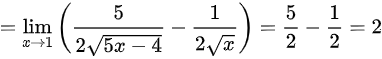 .
.
解析
- 因式分解法:当分式极限中分子分母在趋近点处同为零时,优先因式分解约简;
- 无穷大分式极限:分子分母最高次项次数差决定极限值;
- 分式运算化简:通分合并后约分简化表达式;
- 等价无穷小替换:$\sqrt{x+1}-1 \sim \frac{1}{2}x$;
- 洛必达法则:适用于$\frac{0}{0}$型未定式,通过求导消去不定式。
第(1)题
因式分解
分子:$x^2 + x - 2 = (x+2)(x-1)$
分母:$x^2 - 3x + 2 = (x-2)(x-1)$
约分简化
$\dfrac{(x+2)(x-1)}{(x-2)(x-1)} = \dfrac{x+2}{x-2}$
代入计算
$\lim_{x \to 1} \dfrac{x+2}{x-2} = \dfrac{1+2}{1-2} = -3$
第(2)题
分子分母同除以$x^4$
$\dfrac{x^2 + x}{x^4 - 3x^2 + 1} = \dfrac{\frac{1}{x^2} + \frac{1}{x^3}}{1 - \frac{3}{x^2} + \frac{1}{x^4}}$
利用极限性质
$\lim_{x \to \infty} \dfrac{1}{x^n} = 0$,故极限为$\dfrac{0 + 0}{1 - 0 + 0} = 0$
第(3)题
分母因式分解
$1 - x^3 = (1 - x)(1 + x + x^2)$
通分合并
$\dfrac{1}{1-x} - \dfrac{3}{(1-x)(1+x+x^2)} = \dfrac{1+x+x^2 - 3}{(1-x)(1+x+x^2)}$
化简分子
$1 + x + x^2 - 3 = x^2 + x - 2 = (x+2)(x-1)$
约分代入
$\dfrac{(x+2)(x-1)}{(1-x)(1+x+x^2)} = -\dfrac{x+2}{1+x+x^2}$,代入$x=1$得$-\dfrac{3}{3} = -1$
第(4)题
等价无穷小替换
$\sqrt{x+1} - 1 \sim \dfrac{1}{2}x$
代入计算
$\lim_{x \to 0} \dfrac{\frac{1}{2}x}{x} = \dfrac{1}{2}$
第(5)题
洛必达法则
分子导数:$\dfrac{5}{2\sqrt{5x-4}} - \dfrac{1}{2\sqrt{x}}$
分母导数:$1$
代入计算
$\lim_{x \to 1} \left( \dfrac{5}{2\sqrt{1}} - \dfrac{1}{2\sqrt{1}} \right) = \dfrac{5}{2} - \dfrac{1}{2} = 2$