题目
6.(2024)函数f(x) =dfrac (x+1)({x)^2+x+1}的单调增区间().dfrac (x+1)({x)^2+x+1}
6.(2024)函数f(x) =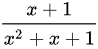 的单调增区间().
的单调增区间().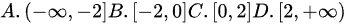
题目解答
答案
解: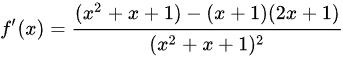
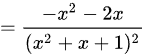 令
令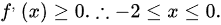 故选 B.
故选 B.
解析
考查要点:本题主要考查利用导数确定函数的单调区间,涉及分式函数的求导法则及二次函数的符号分析。
解题核心思路:
- 求导:使用商的求导法则,计算函数$f(x)$的导数$f'(x)$。
- 分析导数符号:通过分子因式分解确定导数的符号变化,找到$f'(x) \geq 0$的区间。
- 确定单调区间:结合导数的正负性,判断函数的单调递增区间。
破题关键点:
- 分母恒正:分母$(x^2 + x + 1)^2$始终为正,导数符号由分子决定。
- 分子因式分解:将分子$-x^2 - 2x$分解为$-x(x + 2)$,快速确定导数为零的点$x = -2$和$x = 0$。
- 区间测试:通过测试区间内的符号,确定导数的正负性。
步骤1:求导数
函数$f(x) = \dfrac{x + 1}{x^2 + x + 1}$,根据商的求导法则:
$f'(x) = \dfrac{(1)(x^2 + x + 1) - (x + 1)(2x + 1)}{(x^2 + x + 1)^2}$
步骤2:化简分子
展开并整理分子:
$\begin{aligned}\text{分子} &= (x^2 + x + 1) - (x + 1)(2x + 1) \\&= x^2 + x + 1 - (2x^2 + 3x + 1) \\&= -x^2 - 2x.\end{aligned}$
步骤3:确定导数符号
导数为:
$f'(x) = \dfrac{-x^2 - 2x}{(x^2 + x + 1)^2} = \dfrac{-x(x + 2)}{(x^2 + x + 1)^2}.$
分母恒正,分子$-x(x + 2)$的符号由$-x(x + 2)$决定。令分子为零,得临界点$x = -2$和$x = 0$。
步骤4:区间符号分析
- 当$x < -2$时,取测试点$x = -3$,分子为负,$f'(x) < 0$,函数递减。
- 当$-2 < x < 0$时,取测试点$x = -1$,分子为正,$f'(x) > 0$,函数递增。
- 当$x > 0$时,取测试点$x = 1$,分子为负,$f'(x) < 0$,函数递减。
结论:函数$f(x)$的单调递增区间为$[-2, 0]$,对应选项B。