题目
[题目 lim _(xarrow 0)dfrac (ln {(1+x))^dfrac (1{x)-1}}(x)
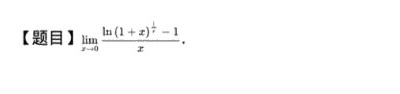
题目解答
答案

解析
步骤 1:化简表达式
原式 $=\lim _{x\rightarrow 0}\dfrac {\ln (1+x)^{\dfrac {1}{x}}-1}{x}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{x}\ln (1+x)-1}{x}=\lim _{x\rightarrow 0}\dfrac {\ln (1+x)-x}{{x}^{2}}$
步骤 2:应用洛必达法则
由于分子和分母在$x\rightarrow 0$时都趋于0,可以应用洛必达法则,即对分子和分母分别求导。
$\lim _{x\rightarrow 0}\dfrac {\ln (1+x)-x}{{x}^{2}}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{1+x}-1}{2x}=\lim _{x\rightarrow 0}\dfrac {1-(1+x)}{2x(1+x)}=\lim _{x\rightarrow 0}\dfrac {-x}{2x(1+x)}$
步骤 3:简化并求极限
$\lim _{x\rightarrow 0}\dfrac {-x}{2x(1+x)}=\lim _{x\rightarrow 0}\dfrac {-1}{2(1+x)}=-\dfrac {1}{2}$
原式 $=\lim _{x\rightarrow 0}\dfrac {\ln (1+x)^{\dfrac {1}{x}}-1}{x}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{x}\ln (1+x)-1}{x}=\lim _{x\rightarrow 0}\dfrac {\ln (1+x)-x}{{x}^{2}}$
步骤 2:应用洛必达法则
由于分子和分母在$x\rightarrow 0$时都趋于0,可以应用洛必达法则,即对分子和分母分别求导。
$\lim _{x\rightarrow 0}\dfrac {\ln (1+x)-x}{{x}^{2}}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{1+x}-1}{2x}=\lim _{x\rightarrow 0}\dfrac {1-(1+x)}{2x(1+x)}=\lim _{x\rightarrow 0}\dfrac {-x}{2x(1+x)}$
步骤 3:简化并求极限
$\lim _{x\rightarrow 0}\dfrac {-x}{2x(1+x)}=\lim _{x\rightarrow 0}\dfrac {-1}{2(1+x)}=-\dfrac {1}{2}$