题目
[题目] lim _(xarrow 0)xsin dfrac (1)(x)

题目解答
答案
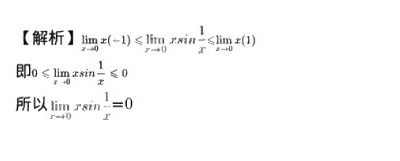
解析
步骤 1:确定函数的定义域
函数 $f(x) = x\sin \dfrac {1}{x}$ 在 $x \neq 0$ 时有定义,因为 $\sin \dfrac {1}{x}$ 在 $x \neq 0$ 时有定义。
步骤 2:应用夹逼定理
我们知道 $-1 \leq \sin \dfrac {1}{x} \leq 1$ 对于所有 $x \neq 0$ 成立。因此,我们可以写出:
$$-x \leq x\sin \dfrac {1}{x} \leq x$$
当 $x \rightarrow 0$ 时,$-x$ 和 $x$ 都趋向于 $0$,所以根据夹逼定理,$x\sin \dfrac {1}{x}$ 也趋向于 $0$。
步骤 3:得出结论
根据上述分析,我们得出结论:
$$\lim _{x\rightarrow 0}x\sin \dfrac {1}{x} = 0$$
函数 $f(x) = x\sin \dfrac {1}{x}$ 在 $x \neq 0$ 时有定义,因为 $\sin \dfrac {1}{x}$ 在 $x \neq 0$ 时有定义。
步骤 2:应用夹逼定理
我们知道 $-1 \leq \sin \dfrac {1}{x} \leq 1$ 对于所有 $x \neq 0$ 成立。因此,我们可以写出:
$$-x \leq x\sin \dfrac {1}{x} \leq x$$
当 $x \rightarrow 0$ 时,$-x$ 和 $x$ 都趋向于 $0$,所以根据夹逼定理,$x\sin \dfrac {1}{x}$ 也趋向于 $0$。
步骤 3:得出结论
根据上述分析,我们得出结论:
$$\lim _{x\rightarrow 0}x\sin \dfrac {1}{x} = 0$$