题目
求int dfrac ({ln )^2sqrt (x)}(sqrt {x)}dx
求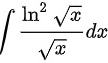
题目解答
答案
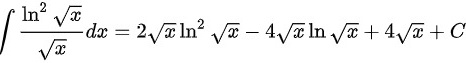
求不定积分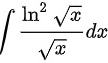
观察其结构,且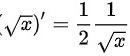
知可先使用第一类换元积分法
则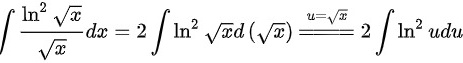
分部积分法
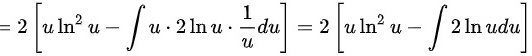
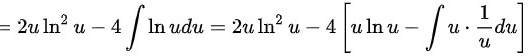
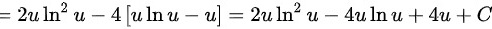
将换元带回
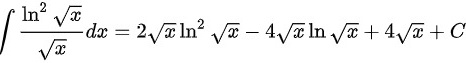
解析
步骤 1:换元
观察积分式子,发现$\sqrt{x}$的导数为$\dfrac{1}{2\sqrt{x}}$,因此可以考虑使用换元法,令$u = \sqrt{x}$,则$du = \dfrac{1}{2\sqrt{x}}dx$,从而$\dfrac{1}{\sqrt{x}}dx = 2du$。
步骤 2:代入换元
将$u = \sqrt{x}$代入原积分式子,得到$\int \dfrac{{\ln}^{2}u}{u} \cdot 2du$。
步骤 3:分部积分
对$\int \dfrac{{\ln}^{2}u}{u} \cdot 2du$进行分部积分,设$v = {\ln}^{2}u$,$dw = \dfrac{2}{u}du$,则$dv = \dfrac{2\ln u}{u}du$,$w = 2\ln u$。
步骤 4:计算分部积分
根据分部积分公式$\int vdw = vw - \int wdv$,计算得到$\int \dfrac{{\ln}^{2}u}{u} \cdot 2du = 2u{\ln}^{2}u - 4\int \ln udu$。
步骤 5:计算剩余积分
对$\int \ln udu$进行分部积分,设$v = \ln u$,$dw = du$,则$dv = \dfrac{1}{u}du$,$w = u$,得到$\int \ln udu = u\ln u - \int du = u\ln u - u$。
步骤 6:代回原变量
将$u = \sqrt{x}$代回,得到$\int \dfrac{{\ln}^{2}\sqrt{x}}{\sqrt{x}}dx = 2\sqrt{x}{\ln}^{2}\sqrt{x} - 4\sqrt{x}\ln \sqrt{x} + 4\sqrt{x} + C$。
观察积分式子,发现$\sqrt{x}$的导数为$\dfrac{1}{2\sqrt{x}}$,因此可以考虑使用换元法,令$u = \sqrt{x}$,则$du = \dfrac{1}{2\sqrt{x}}dx$,从而$\dfrac{1}{\sqrt{x}}dx = 2du$。
步骤 2:代入换元
将$u = \sqrt{x}$代入原积分式子,得到$\int \dfrac{{\ln}^{2}u}{u} \cdot 2du$。
步骤 3:分部积分
对$\int \dfrac{{\ln}^{2}u}{u} \cdot 2du$进行分部积分,设$v = {\ln}^{2}u$,$dw = \dfrac{2}{u}du$,则$dv = \dfrac{2\ln u}{u}du$,$w = 2\ln u$。
步骤 4:计算分部积分
根据分部积分公式$\int vdw = vw - \int wdv$,计算得到$\int \dfrac{{\ln}^{2}u}{u} \cdot 2du = 2u{\ln}^{2}u - 4\int \ln udu$。
步骤 5:计算剩余积分
对$\int \ln udu$进行分部积分,设$v = \ln u$,$dw = du$,则$dv = \dfrac{1}{u}du$,$w = u$,得到$\int \ln udu = u\ln u - \int du = u\ln u - u$。
步骤 6:代回原变量
将$u = \sqrt{x}$代回,得到$\int \dfrac{{\ln}^{2}\sqrt{x}}{\sqrt{x}}dx = 2\sqrt{x}{\ln}^{2}\sqrt{x} - 4\sqrt{x}\ln \sqrt{x} + 4\sqrt{x} + C$。