题目
2分解因式: (x)^4+3(x)^3-6(x)^2-3x+2 .
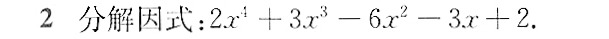
题目解答
答案


解析
考查要点:本题主要考查四次多项式的因式分解能力,特别是当无法直接提取一次因式时,通过分解为两个二次因式乘积的方法。
解题核心思路:
- 试根法排除一次因式:利用有理根定理判断是否存在一次因式,若不存在,则考虑二次因式分解。
- 假设二次因式形式:将多项式分解为两个二次因式的乘积,通过比较系数建立方程组求解参数。
- 整数解的枚举:根据常数项的因数分解,枚举可能的参数组合,代入方程组验证。
破题关键点:
- 有理根定理的应用:通过计算特定值(如$f(1)$、$f(-1)$)排除简单根。
- 二次因式系数的对称性假设:通过合理假设二次因式的系数形式简化计算。
- 方程组的整数解分析:结合常数项的因数分解,枚举可能的整数解,逐步验证。
步骤1:试根法排除一次因式
计算$f(1)=2+3-6-3+2=-2$,$f(-1)=2-3-6+3+2=-2$,说明$x=1$和$x=-1$不是根。进一步根据有理根定理,可能的有理根为$\pm1,\pm2,\pm\frac{1}{2}$,但代入后均不为0,因此原式无一次因式。
步骤2:假设二次因式形式
设原式分解为$(2x^2+ax+b)(x^2+cx+d)$,展开后比较系数:
$\begin{aligned}2x^4 + (a+2c)x^3 + (ac+b+2d)x^2 + (ad+bc)x + bd &= 2x^4 +3x^3-6x^2-3x+2\end{aligned}$
得到方程组:
$\begin{cases}a + 2c = 3 \quad \text{(1)} \\ac + b + 2d = -6 \quad \text{(2)} \\ad + bc = -3 \quad \text{(3)} \\bd = 2 \quad \text{(4)}\end{cases}$
步骤3:枚举常数项因数
由方程(4) $bd=2$,可能的整数解为:
- $(b,d)=(1,2),(2,1),(-1,-2),(-2,-1)$
步骤4:代入验证
以$(b,d)=(-2,-1)$为例:
- 代入方程(2):$ac + (-2) + 2(-1) = -6 \Rightarrow ac = -2$
- 结合方程(1) $a + 2c = 3$,解得$a=-1$, $c=2$
- 验证方程(3):$(-1)(-1) + (-2)(2) = 1 -4 = -3$,成立
步骤5:确定最终分解式
代入$a=-1$, $c=2$, $b=-2$, $d=-1$,得:
$(2x^2 -x -2)(x^2 +2x -1)$