题目
1. =(e)^2x-1 的反函数为 __-|||-2.若 (0)=0. '(0)=2, 则 lim _(harrow 0)dfrac (f(2h))(h)= __
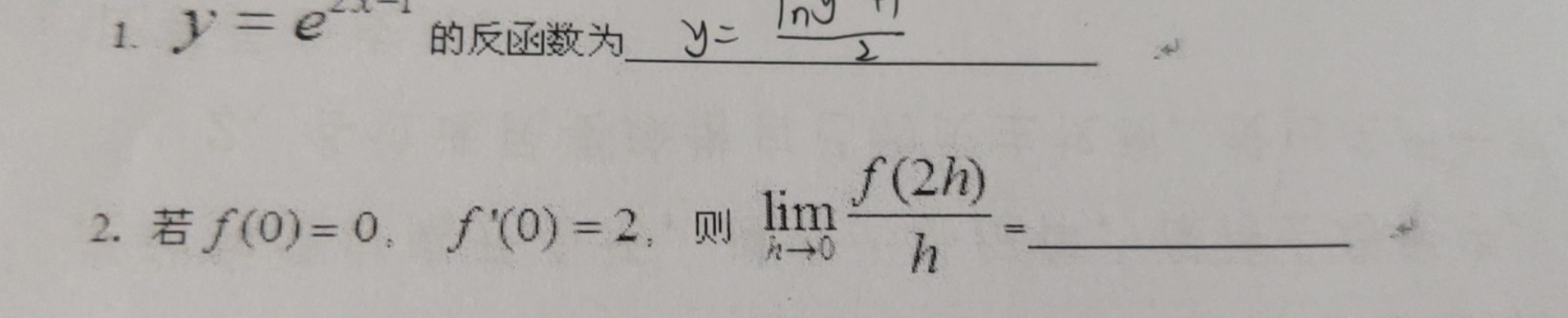
题目解答
答案

解析
- 反函数求解:考查反函数的定义与求解方法,核心是交换原函数的自变量与因变量,解方程得到新的表达式,并注意定义域的变化。
- 导数定义应用:考查导数的定义及极限的转化,关键点在于将给定极限形式转化为已知导数的形式,利用变量替换或直接应用导数定义求解。
第1题:求反函数
交换变量
原函数为 $y = e^{2x-1}$,交换 $x$ 和 $y$,得方程:
$x = e^{2y - 1}$
解方程求 $y$
对等式两边取自然对数:
$\ln x = 2y - 1$
解得:
$y = \frac{\ln x + 1}{2}$
结论:反函数为 $y = \dfrac{\ln x + 1}{2}$,定义域为 $x > 0$。
第2题:求极限
变量替换法
令 $k = 2h$,当 $h \to 0$ 时,$k \to 0$,原极限变为:
$\lim_{k \to 0} \frac{f(k)}{k/2} = 2 \cdot \lim_{k \to 0} \frac{f(k)}{k}$
应用导数定义
根据导数定义:
$\lim_{k \to 0} \frac{f(k) - f(0)}{k} = f'(0) = 2$
由于 $f(0) = 0$,得:
$\lim_{k \to 0} \frac{f(k)}{k} = 2$
因此原极限为:
$2 \cdot 2 = 4$
结论:极限值为 $4$。