题目
11.曲线=dfrac (x)(2)+dfrac (4)(x)在点(2,3)处的切线方程为_________.
11.曲线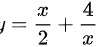
在点(2,3)处的切线方程为_________.
题目解答
答案
答案：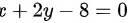
因为
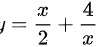
所以
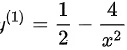
所以函数在点(2,3)处的切线的斜率为
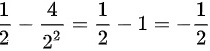
所以切线方程为
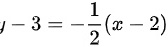
整理得
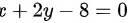
解析
步骤 1：求导数
首先，我们需要求出给定函数$y=\dfrac {x}{2}+\dfrac {4}{x}$的导数，以确定在点(2,3)处的切线斜率。根据导数的定义，我们有：
$y'=\dfrac {d}{dx}\left(\dfrac {x}{2}+\dfrac {4}{x}\right)=\dfrac {1}{2}-\dfrac {4}{{x}^{2}}$
步骤 2：计算切线斜率
将点(2,3)的x坐标代入导数表达式中，计算出在该点处的切线斜率：
$y'(2)=\dfrac {1}{2}-\dfrac {4}{{2}^{2}}=\dfrac {1}{2}-1=-\dfrac {1}{2}$
步骤 3：写出切线方程
根据点斜式方程$y-y_1=m(x-x_1)$，其中$m$是斜率，$(x_1,y_1)$是点的坐标，我们可以写出切线方程：
$y-3=-\dfrac {1}{2}(x-2)$
整理得：
$x+2y-8=0$
首先，我们需要求出给定函数$y=\dfrac {x}{2}+\dfrac {4}{x}$的导数，以确定在点(2,3)处的切线斜率。根据导数的定义，我们有：
$y'=\dfrac {d}{dx}\left(\dfrac {x}{2}+\dfrac {4}{x}\right)=\dfrac {1}{2}-\dfrac {4}{{x}^{2}}$
步骤 2：计算切线斜率
将点(2,3)的x坐标代入导数表达式中，计算出在该点处的切线斜率：
$y'(2)=\dfrac {1}{2}-\dfrac {4}{{2}^{2}}=\dfrac {1}{2}-1=-\dfrac {1}{2}$
步骤 3：写出切线方程
根据点斜式方程$y-y_1=m(x-x_1)$，其中$m$是斜率，$(x_1,y_1)$是点的坐标，我们可以写出切线方程：
$y-3=-\dfrac {1}{2}(x-2)$
整理得：
$x+2y-8=0$