题目
反比例函数(x)=dfrac (3-2m)(x) ，则当 m 满足 _ 时， f ( x ) 是 增函数 .
反比例函数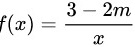
，则当 m 满足 _ 时， f ( x ) 是 增函数 .
题目解答
答案
由于反比例函数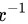
的这一项的符号为负，则 f (x) 是增函数，即当m满足3-2m<0，即m>1.5时，f(x)是增函数。
解析
步骤 1：确定反比例函数的增减性
反比例函数$f(x)=\dfrac {a}{x}$的增减性取决于常数$a$的符号。当$a>0$时，函数在每个象限内是减函数；当$a<0$时，函数在每个象限内是增函数。
步骤 2：确定常数$a$的值
对于给定的反比例函数$f(x)=\dfrac {3-2m}{x}$，常数$a=3-2m$。
步骤 3：确定$m$的取值范围
为了使$f(x)$是增函数，需要$a<0$，即$3-2m<0$。解这个不等式得到$m$的取值范围。
反比例函数$f(x)=\dfrac {a}{x}$的增减性取决于常数$a$的符号。当$a>0$时，函数在每个象限内是减函数；当$a<0$时，函数在每个象限内是增函数。
步骤 2：确定常数$a$的值
对于给定的反比例函数$f(x)=\dfrac {3-2m}{x}$，常数$a=3-2m$。
步骤 3：确定$m$的取值范围
为了使$f(x)$是增函数，需要$a<0$，即$3-2m<0$。解这个不等式得到$m$的取值范围。