题目
(1)已知函数f(x )的定义域为 [ -1,1] , 求函-|||-数 f(2x-1) 的定义域;
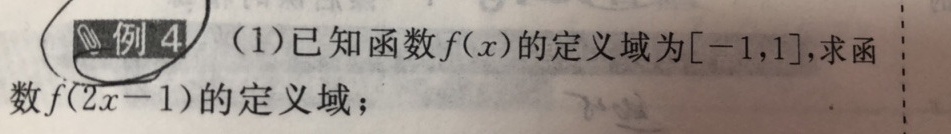
题目解答
答案

解析
步骤 1:理解函数定义域
函数 $f(x)$ 的定义域为 $[-1,1]$,意味着 $x$ 的取值范围是 $-1 \leq x \leq 1$。
步骤 2:确定新函数的定义域
对于函数 $f(2x-1)$,我们需要找到 $2x-1$ 的取值范围,使得 $2x-1$ 落在 $[-1,1]$ 内。即,$-1 \leq 2x-1 \leq 1$。
步骤 3:解不等式
解不等式 $-1 \leq 2x-1 \leq 1$,得到 $0 \leq 2x \leq 2$,进一步得到 $0 \leq x \leq 1$。
函数 $f(x)$ 的定义域为 $[-1,1]$,意味着 $x$ 的取值范围是 $-1 \leq x \leq 1$。
步骤 2:确定新函数的定义域
对于函数 $f(2x-1)$,我们需要找到 $2x-1$ 的取值范围,使得 $2x-1$ 落在 $[-1,1]$ 内。即,$-1 \leq 2x-1 \leq 1$。
步骤 3:解不等式
解不等式 $-1 \leq 2x-1 \leq 1$,得到 $0 \leq 2x \leq 2$,进一步得到 $0 \leq x \leq 1$。