题目
求极限lim _(narrow infty )dfrac (1+3+5+... +(2n-1))({n)^2}=
求极限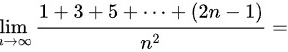
题目解答
答案

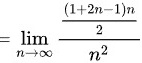
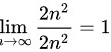
解析
步骤 1:求和公式
首先,我们需要知道等差数列求和的公式。对于等差数列$1, 3, 5, \cdots, (2n-1)$,其首项$a_1=1$,公差$d=2$,项数为$n$。等差数列的求和公式为$S_n=\dfrac{n}{2}[2a_1+(n-1)d]$。将$a_1=1$和$d=2$代入,得到$S_n=\dfrac{n}{2}[2\cdot1+(n-1)\cdot2]=\dfrac{n}{2}[2+2n-2]=\dfrac{n}{2}\cdot2n=n^2$。
步骤 2:代入求极限
将求和公式$S_n=n^2$代入原极限表达式中,得到$\lim _{n\rightarrow \infty }\dfrac {1+3+5+\cdots +(2n-1)}{{n}^{2}}=\lim _{n\rightarrow \infty }\dfrac {n^2}{{n}^{2}}$。
步骤 3:计算极限
计算极限$\lim _{n\rightarrow \infty }\dfrac {n^2}{{n}^{2}}$,由于分子和分母都是$n^2$,所以极限值为$1$。
首先,我们需要知道等差数列求和的公式。对于等差数列$1, 3, 5, \cdots, (2n-1)$,其首项$a_1=1$,公差$d=2$,项数为$n$。等差数列的求和公式为$S_n=\dfrac{n}{2}[2a_1+(n-1)d]$。将$a_1=1$和$d=2$代入,得到$S_n=\dfrac{n}{2}[2\cdot1+(n-1)\cdot2]=\dfrac{n}{2}[2+2n-2]=\dfrac{n}{2}\cdot2n=n^2$。
步骤 2:代入求极限
将求和公式$S_n=n^2$代入原极限表达式中,得到$\lim _{n\rightarrow \infty }\dfrac {1+3+5+\cdots +(2n-1)}{{n}^{2}}=\lim _{n\rightarrow \infty }\dfrac {n^2}{{n}^{2}}$。
步骤 3:计算极限
计算极限$\lim _{n\rightarrow \infty }\dfrac {n^2}{{n}^{2}}$,由于分子和分母都是$n^2$,所以极限值为$1$。