题目
4.设函数f(x,y)可导,且 f(1,-1)=-1 _(1)(1,-1)=2 _(2)'(1,-1)=3, 又 F(x)=-|||-f[x^2,f(x^2,x ^3)],则 '(-1)= __ .
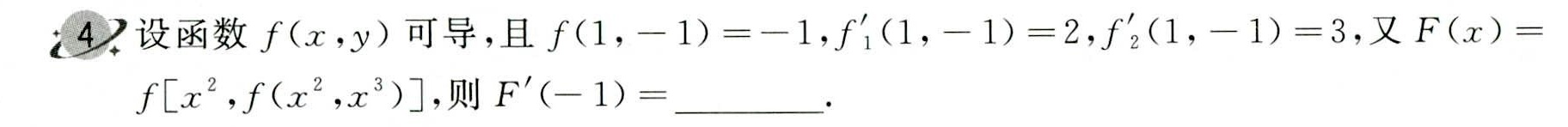
题目解答
答案
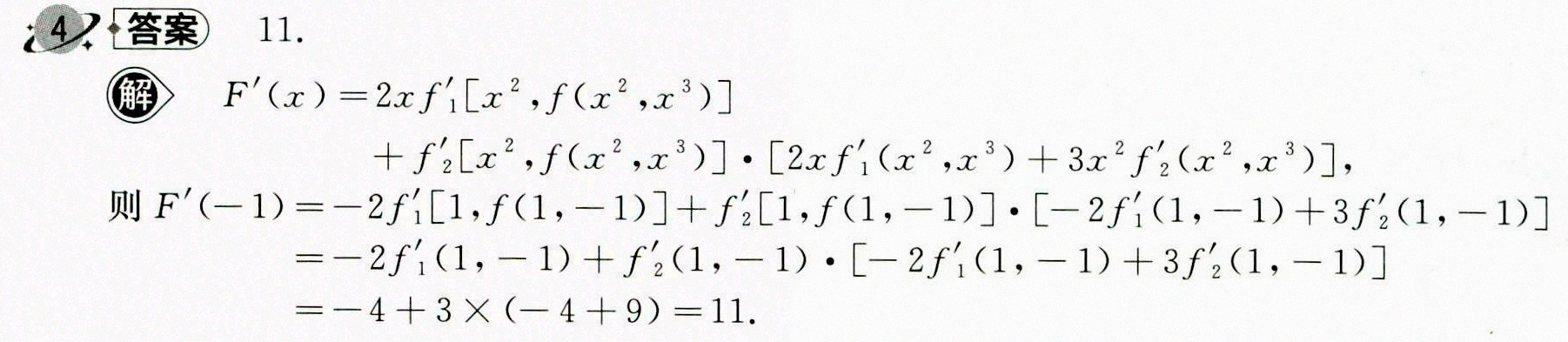
解析
步骤 1:确定函数 F(x) 的形式
函数 F(x) 定义为 F(x) = f[x^2, f(x^2, x^3)],其中 f(x,y) 是一个二元函数。
步骤 2:应用链式法则求导
根据链式法则,F'(x) 可以表示为:
F'(x) = f_1'(x^2, f(x^2, x^3)) * 2x + f_2'(x^2, f(x^2, x^3)) * f_1'(x^2, x^3) * 2x + f_2'(x^2, f(x^2, x^3)) * f_2'(x^2, x^3) * 3x^2
其中,f_1' 和 f_2' 分别表示 f(x,y) 对 x 和 y 的偏导数。
步骤 3:代入 x = -1 并计算 F'(-1)
将 x = -1 代入 F'(x) 的表达式中,得到:
F'(-1) = f_1'(1, f(1, -1)) * 2(-1) + f_2'(1, f(1, -1)) * f_1'(1, -1) * 2(-1) + f_2'(1, f(1, -1)) * f_2'(1, -1) * 3(-1)^2
根据题目条件,f(1, -1) = -1,f_1'(1, -1) = 2,f_2'(1, -1) = 3,代入上述表达式中,得到:
F'(-1) = 2 * (-2) + 3 * 2 * (-2) + 3 * 3 * 3
F'(-1) = -4 - 12 + 27
F'(-1) = 11
函数 F(x) 定义为 F(x) = f[x^2, f(x^2, x^3)],其中 f(x,y) 是一个二元函数。
步骤 2:应用链式法则求导
根据链式法则,F'(x) 可以表示为:
F'(x) = f_1'(x^2, f(x^2, x^3)) * 2x + f_2'(x^2, f(x^2, x^3)) * f_1'(x^2, x^3) * 2x + f_2'(x^2, f(x^2, x^3)) * f_2'(x^2, x^3) * 3x^2
其中,f_1' 和 f_2' 分别表示 f(x,y) 对 x 和 y 的偏导数。
步骤 3:代入 x = -1 并计算 F'(-1)
将 x = -1 代入 F'(x) 的表达式中,得到:
F'(-1) = f_1'(1, f(1, -1)) * 2(-1) + f_2'(1, f(1, -1)) * f_1'(1, -1) * 2(-1) + f_2'(1, f(1, -1)) * f_2'(1, -1) * 3(-1)^2
根据题目条件,f(1, -1) = -1,f_1'(1, -1) = 2,f_2'(1, -1) = 3,代入上述表达式中,得到:
F'(-1) = 2 * (-2) + 3 * 2 * (-2) + 3 * 3 * 3
F'(-1) = -4 - 12 + 27
F'(-1) = 11