题目
求下列极限:lim _(xarrow 1)(dfrac (3)(1-{x)^3}-dfrac (1)(1-x))-|||-__
求下列极限: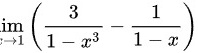
题目解答
答案
首先,将式子进行通分: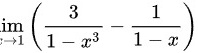
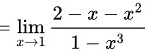 ,用公因式
,用公因式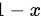 进行约分,则得到:
进行约分,则得到: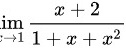
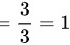 ,最终结果为1
,最终结果为1
解析
步骤 1:通分
将给定的极限式子进行通分,得到一个共同的分母。由于$1-x^3$可以分解为$(1-x)(1+x+x^2)$,因此可以将两个分数的分母统一为$1-x^3$。
步骤 2:合并分子
将通分后的分子进行合并,得到一个新的分子表达式。
步骤 3:约分
由于分子和分母都含有$(1-x)$的因子,可以进行约分,简化表达式。
步骤 4:求极限
将简化后的表达式代入$x=1$,求出极限值。
将给定的极限式子进行通分,得到一个共同的分母。由于$1-x^3$可以分解为$(1-x)(1+x+x^2)$,因此可以将两个分数的分母统一为$1-x^3$。
步骤 2:合并分子
将通分后的分子进行合并,得到一个新的分子表达式。
步骤 3:约分
由于分子和分母都含有$(1-x)$的因子,可以进行约分,简化表达式。
步骤 4:求极限
将简化后的表达式代入$x=1$,求出极限值。