题目
已知函数 f(x)在 (0,+infty ) 内可导, (x)gt 0, lim _(xarrow +infty )f(x)=1, 且满足 lim _(harrow 0)([ dfrac {f(x+hx))(f(x))] }^dfrac (1{n)}-|||-=(e)^dfrac (1{x)}, 求 f(x)所满足的方程.
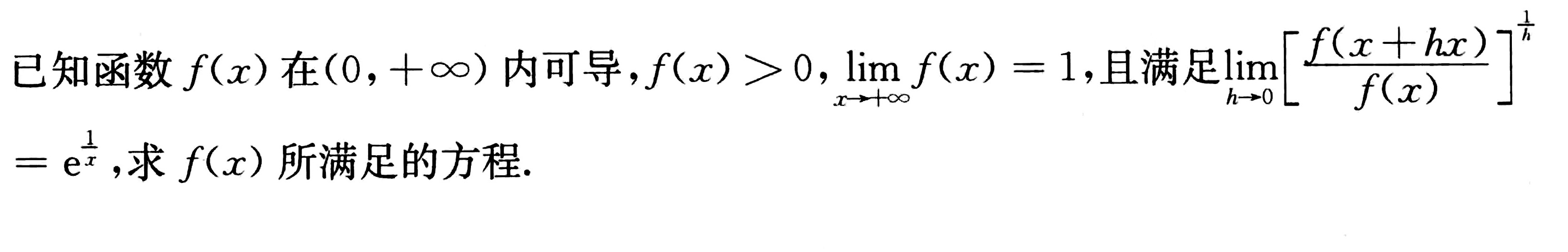
题目解答
答案

解析
步骤 1:定义变量
设 $y={[ \dfrac {f(x+hx)}{f(x)}] }^{\dfrac {1}{h}}$ ,其中 $h$ 是一个趋近于0的变量,$x$ 是函数的自变量。
步骤 2:对数变换
对 $y$ 取自然对数,得到 $\ln y=\dfrac {1}{h}\ln \dfrac {f(x+hx)}{f(x)}$。
步骤 3:求极限
求 $\lim _{h\rightarrow 0}\ln y$,即求 $\lim _{h\rightarrow 0}\dfrac {1}{h}\ln \dfrac {f(x+hx)}{f(x)}$。根据洛必达法则,可以将极限转换为导数的形式,即 $\lim _{h\rightarrow 0}\dfrac {1}{h}\ln \dfrac {f(x+hx)}{f(x)} = \lim _{h\rightarrow 0} \dfrac{\ln f(x+hx) - \ln f(x)}{h} = \dfrac{d}{dx} \ln f(x)$。
步骤 4:应用已知条件
根据题目条件,$\lim _{h\rightarrow 0}{[ \dfrac {f(x+hx)}{f(x)}] }^{\dfrac {1}{h}}={e}^{\dfrac {1}{x}}$,因此 $\lim _{h\rightarrow 0}\ln y = \dfrac{1}{x}$。
步骤 5:求解微分方程
由步骤 4 可知,$\dfrac{d}{dx} \ln f(x) = \dfrac{1}{x}$,即 $\ln f(x) = \int \dfrac{1}{x} dx = \ln x + C$,其中 $C$ 是积分常数。因此,$f(x) = e^{\ln x + C} = C'x$,其中 $C' = e^C$。
步骤 6:确定常数
根据题目条件 $\lim _{x\rightarrow +\infty }f(x)=1$,可以确定 $C' = 1$,因此 $f(x) = e^{-\dfrac{1}{x}}$。
设 $y={[ \dfrac {f(x+hx)}{f(x)}] }^{\dfrac {1}{h}}$ ,其中 $h$ 是一个趋近于0的变量,$x$ 是函数的自变量。
步骤 2:对数变换
对 $y$ 取自然对数,得到 $\ln y=\dfrac {1}{h}\ln \dfrac {f(x+hx)}{f(x)}$。
步骤 3:求极限
求 $\lim _{h\rightarrow 0}\ln y$,即求 $\lim _{h\rightarrow 0}\dfrac {1}{h}\ln \dfrac {f(x+hx)}{f(x)}$。根据洛必达法则,可以将极限转换为导数的形式,即 $\lim _{h\rightarrow 0}\dfrac {1}{h}\ln \dfrac {f(x+hx)}{f(x)} = \lim _{h\rightarrow 0} \dfrac{\ln f(x+hx) - \ln f(x)}{h} = \dfrac{d}{dx} \ln f(x)$。
步骤 4:应用已知条件
根据题目条件,$\lim _{h\rightarrow 0}{[ \dfrac {f(x+hx)}{f(x)}] }^{\dfrac {1}{h}}={e}^{\dfrac {1}{x}}$,因此 $\lim _{h\rightarrow 0}\ln y = \dfrac{1}{x}$。
步骤 5:求解微分方程
由步骤 4 可知,$\dfrac{d}{dx} \ln f(x) = \dfrac{1}{x}$,即 $\ln f(x) = \int \dfrac{1}{x} dx = \ln x + C$,其中 $C$ 是积分常数。因此,$f(x) = e^{\ln x + C} = C'x$,其中 $C' = e^C$。
步骤 6:确定常数
根据题目条件 $\lim _{x\rightarrow +\infty }f(x)=1$,可以确定 $C' = 1$,因此 $f(x) = e^{-\dfrac{1}{x}}$。