题目
int dfrac ({e)^x}({2)^x}dx;
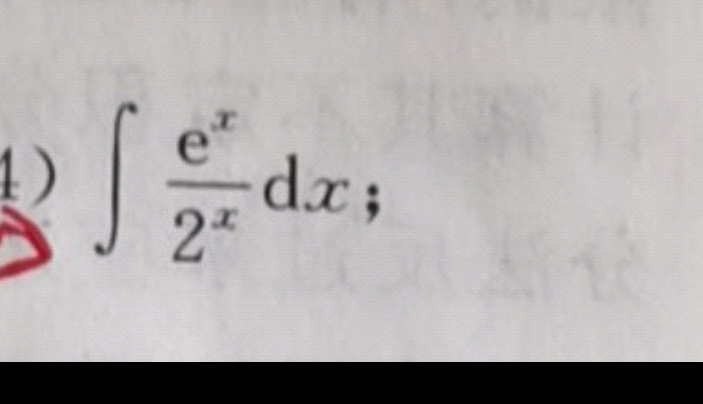
题目解答
答案
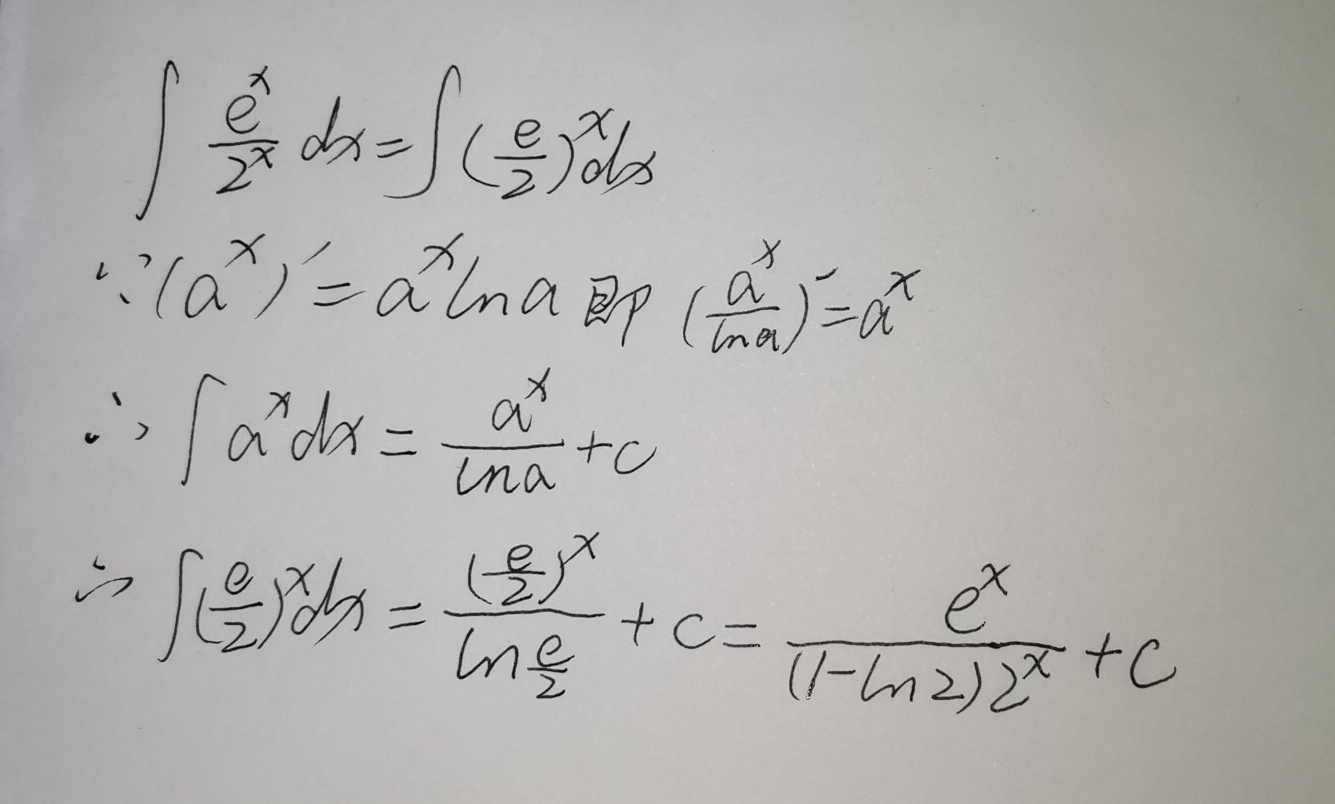
解析
步骤 1:化简被积函数
将被积函数 $\dfrac{{e}^{x}}{{2}^{x}}$ 化简为 ${(\dfrac{e}{2})}^{x}$,因为 ${e}^{x} = {2}^{x} \cdot {(\dfrac{e}{2})}^{x}$。
步骤 2:应用指数函数的积分公式
根据指数函数的积分公式 ${\int }_{{a}^{x}dx} = \dfrac{{a}^{x}}{\ln a} + c$,其中 $a = \dfrac{e}{2}$,我们有 ${\int }_{{(\dfrac{e}{2})}^{x}dx} = \dfrac{{(\dfrac{e}{2})}^{x}}{\ln(\dfrac{e}{2})} + c$。
步骤 3:计算 $\ln(\dfrac{e}{2})$
$\ln(\dfrac{e}{2}) = \ln(e) - \ln(2) = 1 - \ln(2)$。
步骤 4:代入并简化
将 $\ln(\dfrac{e}{2})$ 的值代入积分公式,得到 $\dfrac{{(\dfrac{e}{2})}^{x}}{1 - \ln(2)} + c$。
将被积函数 $\dfrac{{e}^{x}}{{2}^{x}}$ 化简为 ${(\dfrac{e}{2})}^{x}$,因为 ${e}^{x} = {2}^{x} \cdot {(\dfrac{e}{2})}^{x}$。
步骤 2:应用指数函数的积分公式
根据指数函数的积分公式 ${\int }_{{a}^{x}dx} = \dfrac{{a}^{x}}{\ln a} + c$,其中 $a = \dfrac{e}{2}$,我们有 ${\int }_{{(\dfrac{e}{2})}^{x}dx} = \dfrac{{(\dfrac{e}{2})}^{x}}{\ln(\dfrac{e}{2})} + c$。
步骤 3:计算 $\ln(\dfrac{e}{2})$
$\ln(\dfrac{e}{2}) = \ln(e) - \ln(2) = 1 - \ln(2)$。
步骤 4:代入并简化
将 $\ln(\dfrac{e}{2})$ 的值代入积分公式,得到 $\dfrac{{(\dfrac{e}{2})}^{x}}{1 - \ln(2)} + c$。