题目
int dfrac (1)({x)^2}sqrt (dfrac {1-x)(1+x)}dx
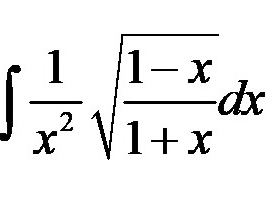
题目解答
答案
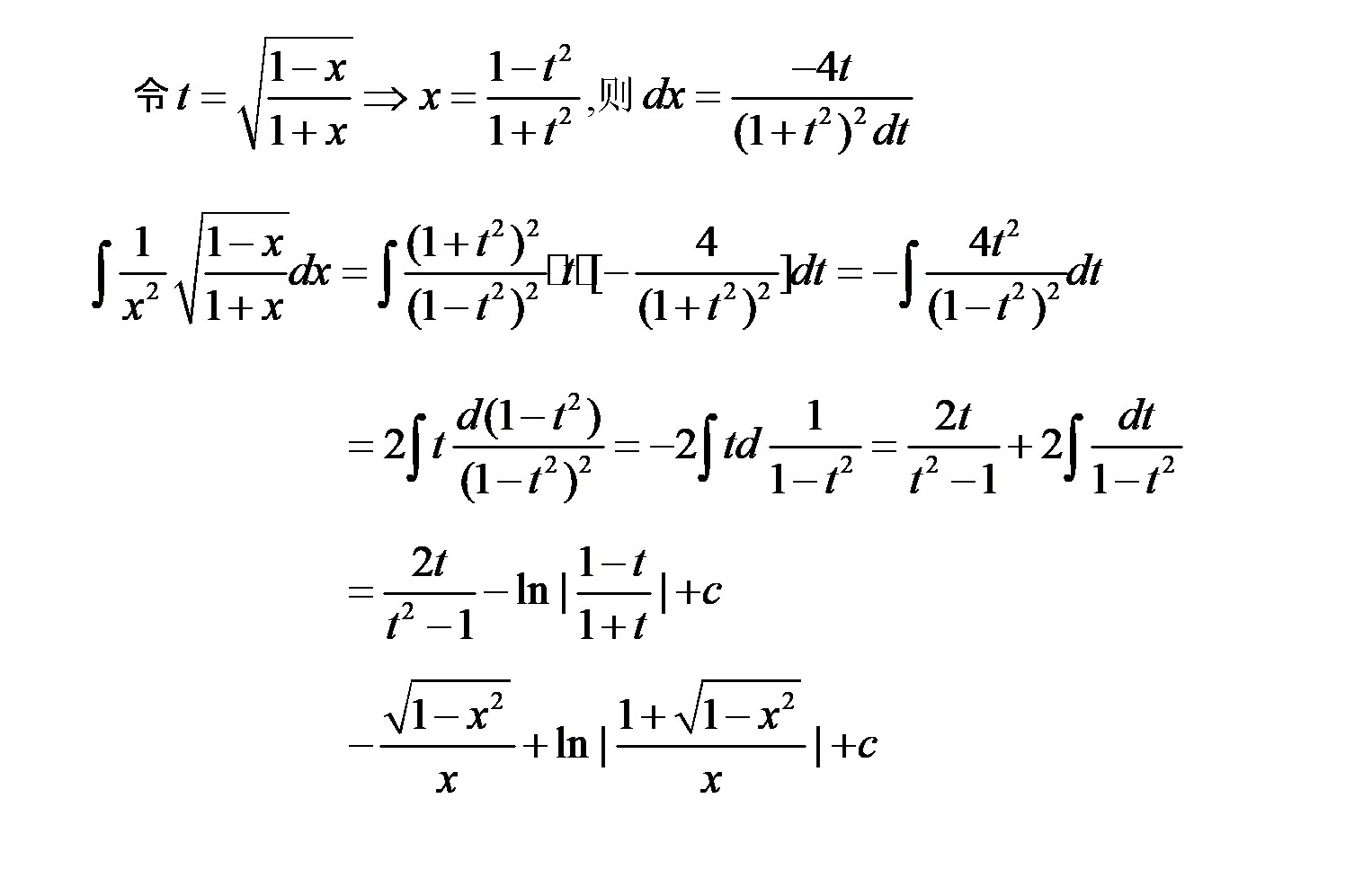
解析
步骤 1:变量替换
令 $t=\sqrt {\dfrac {1-x}{1+x}}$,则 $x=\dfrac {1-{t}^{2}}{1+{t}^{2}}$。对 $x$ 求导,得到 $dx=\dfrac {-4t}{{(1+{t}^{2})}^{2}}dt$。
步骤 2:代入积分
将 $x$ 和 $dx$ 的表达式代入原积分,得到 $\int \dfrac {1}{{x}^{2}}\sqrt {\dfrac {1-x}{1+x}}dx = \int \dfrac {1}{{(\dfrac {1-{t}^{2}}{1+{t}^{2}})}^{2}}\cdot t\cdot \dfrac {-4t}{{(1+{t}^{2})}^{2}}dt$。
步骤 3:化简积分
化简得到 $\int \dfrac {1}{{(\dfrac {1-{t}^{2}}{1+{t}^{2}})}^{2}}\cdot t\cdot \dfrac {-4t}{{(1+{t}^{2})}^{2}}dt = 2\int \dfrac {d(1-{t}^{2})}{{(1-{t}^{2})}^{2}}$。
步骤 4:分部积分
$2\int \dfrac {d(1-{t}^{2})}{{(1-{t}^{2})}^{2}} = -2\int td\dfrac {1}{1-{t}^{2}} = \dfrac {2t}{{t}^{2}-1}+2\int \dfrac {dt}{1-{t}^{2}}$。
步骤 5:积分求解
$\dfrac {2t}{{t}^{2}-1}+2\int \dfrac {dt}{1-{t}^{2}} = \dfrac {2t}{{t}^{2}-1}-\ln |\dfrac {1-t}{1+t}|+c$。
步骤 6:反代入
将 $t=\sqrt {\dfrac {1-x}{1+x}}$ 代入,得到 $-\dfrac {\sqrt {1-{x}^{2}}}{x}+\ln |\dfrac {1+\sqrt {1-{x}^{2}}}{x}|+c$。
令 $t=\sqrt {\dfrac {1-x}{1+x}}$,则 $x=\dfrac {1-{t}^{2}}{1+{t}^{2}}$。对 $x$ 求导,得到 $dx=\dfrac {-4t}{{(1+{t}^{2})}^{2}}dt$。
步骤 2:代入积分
将 $x$ 和 $dx$ 的表达式代入原积分,得到 $\int \dfrac {1}{{x}^{2}}\sqrt {\dfrac {1-x}{1+x}}dx = \int \dfrac {1}{{(\dfrac {1-{t}^{2}}{1+{t}^{2}})}^{2}}\cdot t\cdot \dfrac {-4t}{{(1+{t}^{2})}^{2}}dt$。
步骤 3:化简积分
化简得到 $\int \dfrac {1}{{(\dfrac {1-{t}^{2}}{1+{t}^{2}})}^{2}}\cdot t\cdot \dfrac {-4t}{{(1+{t}^{2})}^{2}}dt = 2\int \dfrac {d(1-{t}^{2})}{{(1-{t}^{2})}^{2}}$。
步骤 4:分部积分
$2\int \dfrac {d(1-{t}^{2})}{{(1-{t}^{2})}^{2}} = -2\int td\dfrac {1}{1-{t}^{2}} = \dfrac {2t}{{t}^{2}-1}+2\int \dfrac {dt}{1-{t}^{2}}$。
步骤 5:积分求解
$\dfrac {2t}{{t}^{2}-1}+2\int \dfrac {dt}{1-{t}^{2}} = \dfrac {2t}{{t}^{2}-1}-\ln |\dfrac {1-t}{1+t}|+c$。
步骤 6:反代入
将 $t=\sqrt {\dfrac {1-x}{1+x}}$ 代入,得到 $-\dfrac {\sqrt {1-{x}^{2}}}{x}+\ln |\dfrac {1+\sqrt {1-{x}^{2}}}{x}|+c$。