题目
1.计算下列极限:-|||-(1) lim _(xarrow 0)dfrac (sin 3x)(sin 5x)
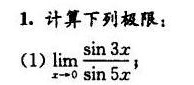
题目解答
答案
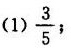
解析
考查要点:本题主要考查等价无穷小替换或洛必达法则的应用,属于极限计算中的常见题型。
解题核心思路:
当$x \rightarrow 0$时,$\sin kx \sim kx$(其中$k$为常数),这是等价无穷小替换的典型应用。直接替换后可快速求解。
若使用洛必达法则,需注意原式为$\frac{0}{0}$型不定式,对分子分母分别求导后化简即可。
破题关键点:
- 识别极限形式为$\frac{0}{0}$型,选择合适的方法。
- 熟练应用等价无穷小或洛必达法则简化计算。
方法一:等价无穷小替换
当$x \rightarrow 0$时,$\sin 3x \sim 3x$,$\sin 5x \sim 5x$,因此:
$\lim _{x\rightarrow 0}\dfrac {\sin 3x}{\sin 5x} = \lim _{x\rightarrow 0}\dfrac{3x}{5x} = \dfrac{3}{5}.$
方法二:洛必达法则
原式为$\frac{0}{0}$型不定式,对分子分母分别求导:
$\lim _{x\rightarrow 0}\dfrac{\sin 3x}{\sin 5x} = \lim _{x\rightarrow 0}\dfrac{(3\cos 3x)}{(5\cos 5x)} = \dfrac{3 \cdot 1}{5 \cdot 1} = \dfrac{3}{5}.$