题目
求函数(x)=2(x)^2-ln x的单调区间和极值.
求函数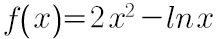
的单调区间和极值.
题目解答
答案
由题意得：定义域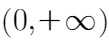
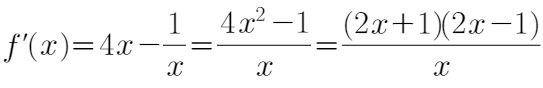
令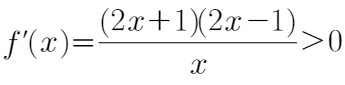
解得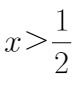
或
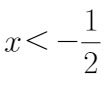(舍去)
单调递增区间为
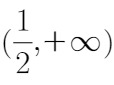，单调递减区间为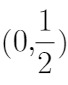
当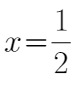
时，取极小值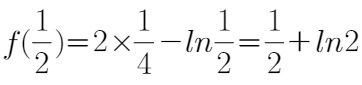
综上所述，结论为：单调递增区间为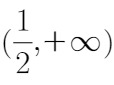，单调递减区间为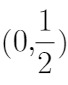；极小值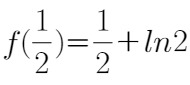
解析
步骤 1：求导数
首先，我们需要求出函数$f(x)=2{x}^{2}-\ln x$的导数$f'(x)$。根据导数的定义和求导法则，我们有：
$$f'(x) = \frac{d}{dx}(2x^2) - \frac{d}{dx}(\ln x) = 4x - \frac{1}{x}$$
步骤 2：确定导数的符号
为了确定函数的单调性，我们需要分析导数$f'(x)$的符号。我们有：
$$f'(x) = 4x - \frac{1}{x} = \frac{4x^2 - 1}{x} = \frac{(2x + 1)(2x - 1)}{x}$$
由于函数的定义域为$(0, +\infty)$，我们只考虑$x > 0$的情况。因此，我们只需要分析分子$(2x + 1)(2x - 1)$的符号。显然，当$x > \frac{1}{2}$时，$f'(x) > 0$；当$0 < x < \frac{1}{2}$时，$f'(x) < 0$。
步骤 3：确定单调区间和极值
根据$f'(x)$的符号，我们可以确定函数的单调区间。当$f'(x) > 0$时，函数单调递增；当$f'(x) < 0$时，函数单调递减。因此，函数$f(x)$在$(0, \frac{1}{2})$上单调递减，在$(\frac{1}{2}, +\infty)$上单调递增。当$x = \frac{1}{2}$时，函数$f(x)$取得极小值。
首先，我们需要求出函数$f(x)=2{x}^{2}-\ln x$的导数$f'(x)$。根据导数的定义和求导法则，我们有：
$$f'(x) = \frac{d}{dx}(2x^2) - \frac{d}{dx}(\ln x) = 4x - \frac{1}{x}$$
步骤 2：确定导数的符号
为了确定函数的单调性，我们需要分析导数$f'(x)$的符号。我们有：
$$f'(x) = 4x - \frac{1}{x} = \frac{4x^2 - 1}{x} = \frac{(2x + 1)(2x - 1)}{x}$$
由于函数的定义域为$(0, +\infty)$，我们只考虑$x > 0$的情况。因此，我们只需要分析分子$(2x + 1)(2x - 1)$的符号。显然，当$x > \frac{1}{2}$时，$f'(x) > 0$；当$0 < x < \frac{1}{2}$时，$f'(x) < 0$。
步骤 3：确定单调区间和极值
根据$f'(x)$的符号，我们可以确定函数的单调区间。当$f'(x) > 0$时，函数单调递增；当$f'(x) < 0$时，函数单调递减。因此，函数$f(x)$在$(0, \frac{1}{2})$上单调递减，在$(\frac{1}{2}, +\infty)$上单调递增。当$x = \frac{1}{2}$时，函数$f(x)$取得极小值。