题目
(2021年2)已知 (x)=dfrac (x|x|)(1+x) 求f(x)的凹凸区间及渐近线.
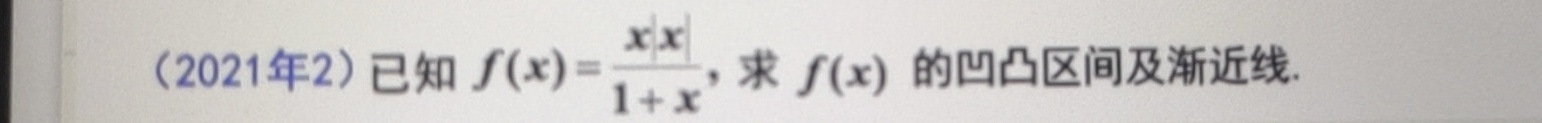
题目解答
答案

解析
步骤 1:求导数
首先,我们需要求出函数 $f(x)=\dfrac {x|x|}{1+x}$ 的一阶导数 $f'(x)$ 和二阶导数 $f''(x)$,以确定函数的凹凸区间。
- 当 $x\geqslant 0$ 时,$f(x)=\dfrac {x^2}{1+x}$,则 $f'(x)=\dfrac {2x(1+x)-x^2}{(1+x)^2}=\dfrac {x^2+2x}{(1+x)^2}$,$f''(x)=\dfrac {2(1+x)^2-(x^2+2x)2(1+x)}{(1+x)^4}=\dfrac {2(1+x)-2(x^2+2x)}{(1+x)^3}=\dfrac {2-2x^2}{(1+x)^3}$。
- 当 $x<0$ 时,$f(x)=\dfrac {-x^2}{1+x}$,则 $f'(x)=\dfrac {-2x(1+x)+x^2}{(1+x)^2}=\dfrac {-x^2-2x}{(1+x)^2}$,$f''(x)=\dfrac {-2(1+x)^2+(x^2+2x)2(1+x)}{(1+x)^4}=\dfrac {-2(1+x)+2(x^2+2x)}{(1+x)^3}=\dfrac {-2+2x^2}{(1+x)^3}$。
步骤 2:确定凹凸区间
- 当 $x\geqslant 0$ 时,$f''(x)=\dfrac {2-2x^2}{(1+x)^3}$,令 $f''(x)=0$,解得 $x=1$,则 $x\in(0,1)$ 时,$f''(x)>0$,函数为凹区间;$x\in(1,+\infty)$ 时,$f''(x)<0$,函数为凸区间。
- 当 $x<0$ 时,$f''(x)=\dfrac {-2+2x^2}{(1+x)^3}$,令 $f''(x)=0$,解得 $x=-1$,则 $x\in(-\infty,-1)$ 时,$f''(x)<0$,函数为凸区间;$x\in(-1,0)$ 时,$f''(x)>0$,函数为凹区间。
步骤 3:求渐近线
- 水平渐近线:$\lim _{x\rightarrow \pm \infty }\dfrac {f(x)}{x}=\lim _{x\rightarrow \pm \infty }\dfrac {|x|}{1+x}=\lim _{x\rightarrow \pm \infty }\dfrac {1}{\dfrac {1}{|x|}+\dfrac {1}{x}}=1$,所以水平渐近线为 $y=x$。
- 垂直渐近线:$\lim _{x\rightarrow -1}f(x)=\lim _{x\rightarrow -1}\dfrac {x|x|}{1+x}=\lim _{x\rightarrow -1}\dfrac {-x^2}{1+x}=-\infty$,所以垂直渐近线为 $x=-1$。
首先,我们需要求出函数 $f(x)=\dfrac {x|x|}{1+x}$ 的一阶导数 $f'(x)$ 和二阶导数 $f''(x)$,以确定函数的凹凸区间。
- 当 $x\geqslant 0$ 时,$f(x)=\dfrac {x^2}{1+x}$,则 $f'(x)=\dfrac {2x(1+x)-x^2}{(1+x)^2}=\dfrac {x^2+2x}{(1+x)^2}$,$f''(x)=\dfrac {2(1+x)^2-(x^2+2x)2(1+x)}{(1+x)^4}=\dfrac {2(1+x)-2(x^2+2x)}{(1+x)^3}=\dfrac {2-2x^2}{(1+x)^3}$。
- 当 $x<0$ 时,$f(x)=\dfrac {-x^2}{1+x}$,则 $f'(x)=\dfrac {-2x(1+x)+x^2}{(1+x)^2}=\dfrac {-x^2-2x}{(1+x)^2}$,$f''(x)=\dfrac {-2(1+x)^2+(x^2+2x)2(1+x)}{(1+x)^4}=\dfrac {-2(1+x)+2(x^2+2x)}{(1+x)^3}=\dfrac {-2+2x^2}{(1+x)^3}$。
步骤 2:确定凹凸区间
- 当 $x\geqslant 0$ 时,$f''(x)=\dfrac {2-2x^2}{(1+x)^3}$,令 $f''(x)=0$,解得 $x=1$,则 $x\in(0,1)$ 时,$f''(x)>0$,函数为凹区间;$x\in(1,+\infty)$ 时,$f''(x)<0$,函数为凸区间。
- 当 $x<0$ 时,$f''(x)=\dfrac {-2+2x^2}{(1+x)^3}$,令 $f''(x)=0$,解得 $x=-1$,则 $x\in(-\infty,-1)$ 时,$f''(x)<0$,函数为凸区间;$x\in(-1,0)$ 时,$f''(x)>0$,函数为凹区间。
步骤 3:求渐近线
- 水平渐近线:$\lim _{x\rightarrow \pm \infty }\dfrac {f(x)}{x}=\lim _{x\rightarrow \pm \infty }\dfrac {|x|}{1+x}=\lim _{x\rightarrow \pm \infty }\dfrac {1}{\dfrac {1}{|x|}+\dfrac {1}{x}}=1$,所以水平渐近线为 $y=x$。
- 垂直渐近线:$\lim _{x\rightarrow -1}f(x)=\lim _{x\rightarrow -1}\dfrac {x|x|}{1+x}=\lim _{x\rightarrow -1}\dfrac {-x^2}{1+x}=-\infty$,所以垂直渐近线为 $x=-1$。