题目
(2) (int )_(-2)^1dfrac (dx)({(11+5x))^3} :
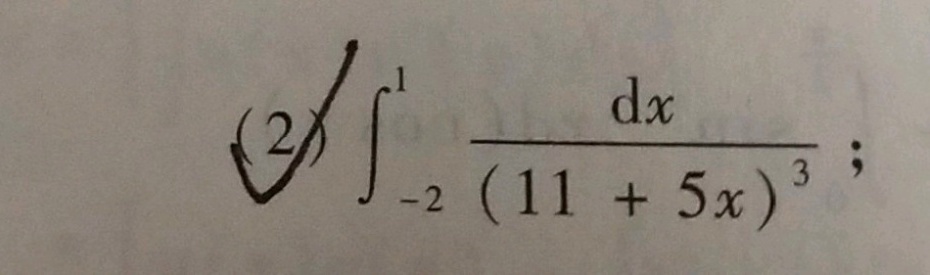
题目解答
答案
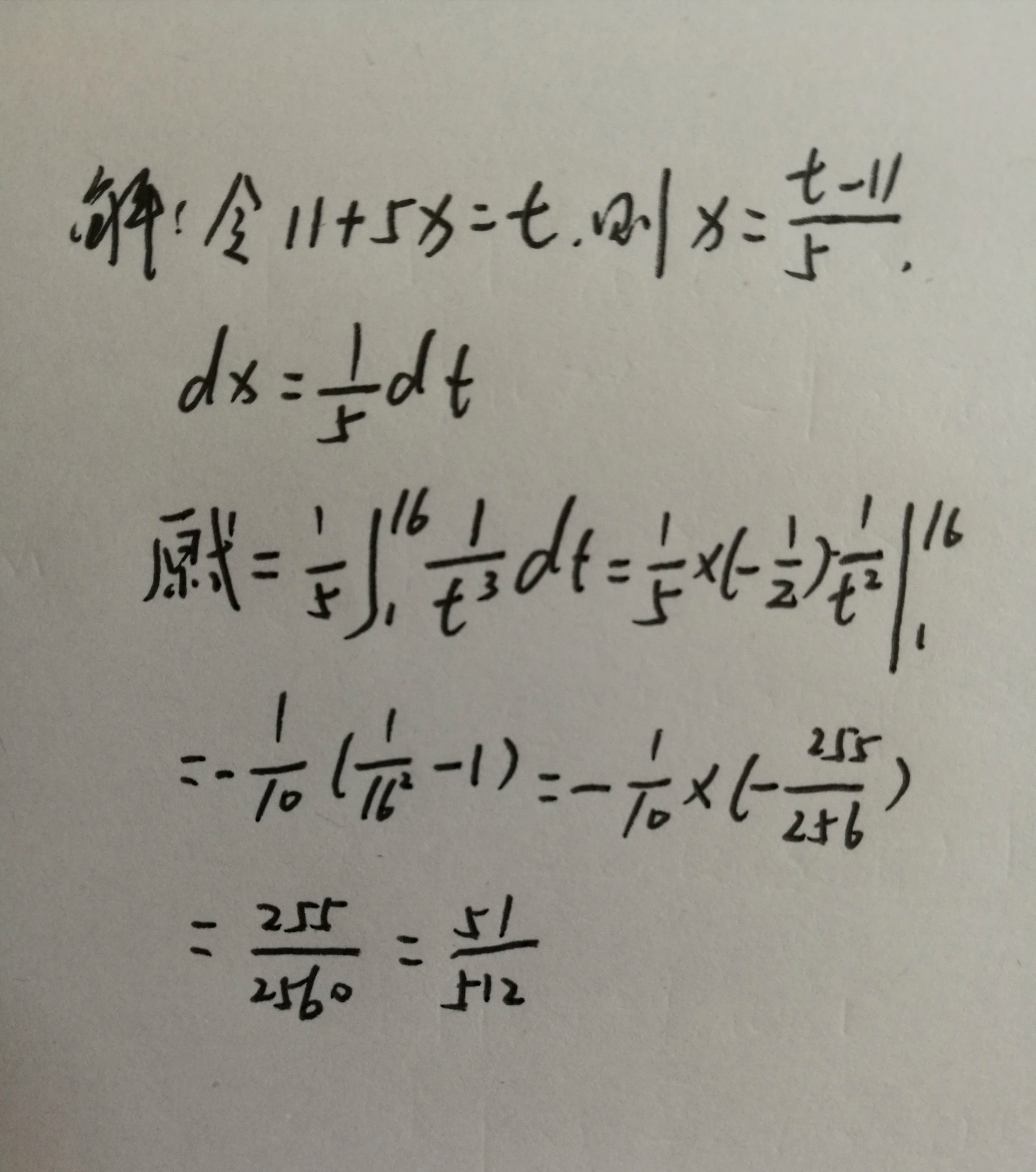
解析
步骤 1:变量替换
令 $t = 11 + 5x$,则 $x = \dfrac{t - 11}{5}$,$dx = \dfrac{1}{5}dt$。
步骤 2:积分变换
原式变为 $\dfrac{1}{5}{\int }_{1}^{16}\dfrac {1}{{t}^{3}}dt$。
步骤 3:积分计算
计算积分 $\dfrac{1}{5}{\int }_{1}^{16}\dfrac {1}{{t}^{3}}dt = \dfrac{1}{5} \times (-\dfrac{1}{2})\dfrac{1}{{t}^{2}}{\int }_{1}^{16}$。
步骤 4:代入上下限
代入上下限 $t = 16$ 和 $t = 1$,得到 $-\dfrac{1}{10}(\dfrac{1}{{16}^{2}} - 1)$。
步骤 5:简化结果
简化结果得到 $-\dfrac{1}{10} \times (-\dfrac{255}{256}) = \dfrac{255}{2560} = \dfrac{51}{512}$。
令 $t = 11 + 5x$,则 $x = \dfrac{t - 11}{5}$,$dx = \dfrac{1}{5}dt$。
步骤 2:积分变换
原式变为 $\dfrac{1}{5}{\int }_{1}^{16}\dfrac {1}{{t}^{3}}dt$。
步骤 3:积分计算
计算积分 $\dfrac{1}{5}{\int }_{1}^{16}\dfrac {1}{{t}^{3}}dt = \dfrac{1}{5} \times (-\dfrac{1}{2})\dfrac{1}{{t}^{2}}{\int }_{1}^{16}$。
步骤 4:代入上下限
代入上下限 $t = 16$ 和 $t = 1$,得到 $-\dfrac{1}{10}(\dfrac{1}{{16}^{2}} - 1)$。
步骤 5:简化结果
简化结果得到 $-\dfrac{1}{10} \times (-\dfrac{255}{256}) = \dfrac{255}{2560} = \dfrac{51}{512}$。