题目
求极限 lim _(xarrow 1)(1-(x)^2)tan dfrac (pi )(2)x
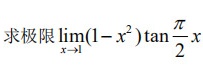
题目解答
答案
解析: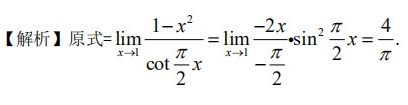
解析
步骤 1:将原式转换为可求导的形式
原式 $=\lim _{x\rightarrow 1}\dfrac {1-{x}^{2}}{\cot \dfrac {\pi }{2}x}$,因为当$x\rightarrow 1$时,$1-x^2\rightarrow 0$,$\cot \dfrac {\pi }{2}x\rightarrow 0$,所以可以使用洛必达法则。
步骤 2:应用洛必达法则
对分子和分母分别求导,得到 $\lim _{x\rightarrow 1}\dfrac {-2x}{-\dfrac {\pi }{2}{\sin }^{2}\dfrac {\pi }{2}x}$。
步骤 3:简化表达式
将$x=1$代入上式,得到 $\dfrac {-2}{-\dfrac {\pi }{2}{\sin }^{2}\dfrac {\pi }{2}}=\dfrac {4}{\pi }$。
原式 $=\lim _{x\rightarrow 1}\dfrac {1-{x}^{2}}{\cot \dfrac {\pi }{2}x}$,因为当$x\rightarrow 1$时,$1-x^2\rightarrow 0$,$\cot \dfrac {\pi }{2}x\rightarrow 0$,所以可以使用洛必达法则。
步骤 2:应用洛必达法则
对分子和分母分别求导,得到 $\lim _{x\rightarrow 1}\dfrac {-2x}{-\dfrac {\pi }{2}{\sin }^{2}\dfrac {\pi }{2}x}$。
步骤 3:简化表达式
将$x=1$代入上式,得到 $\dfrac {-2}{-\dfrac {\pi }{2}{\sin }^{2}\dfrac {\pi }{2}}=\dfrac {4}{\pi }$。