题目
f(x)= ), xlt 0 ln (1+x),xgeqslant 0 . 在 x=0 处的连续性.
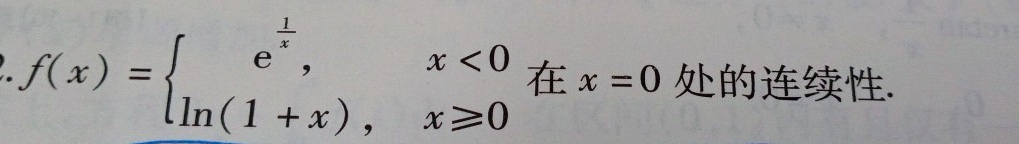
题目解答
答案
解析
步骤 1:定义函数在 x=0 处的左极限和右极限
函数 f(x) 在 x=0 处的左极限为 $\lim _{x\rightarrow 0^{-}}f(x)=\lim _{x\rightarrow 0^{-}}{e}^{\dfrac {1}{x}}$,右极限为 $\lim _{x\rightarrow 0^{+}}f(x)=\lim _{x\rightarrow 0^{+}}\ln (1+x)$。
步骤 2:计算左极限
当 x 趋近于 0 的左侧时,$\dfrac {1}{x}$ 趋近于负无穷大,因此 ${e}^{\dfrac {1}{x}}$ 趋近于 0。所以,$\lim _{x\rightarrow 0^{-}}f(x)=0$。
步骤 3:计算右极限
当 x 趋近于 0 的右侧时,$\ln (1+x)$ 趋近于 $\ln (1+0)=\ln 1=0$。所以,$\lim _{x\rightarrow 0^{+}}f(x)=0$。
步骤 4:判断函数在 x=0 处的连续性
由于 $\lim _{x\rightarrow 0^{-}}f(x)=\lim _{x\rightarrow 0^{+}}f(x)=0$,且 f(0)=ln(1+0)=0,所以函数 f(x) 在 x=0 处是连续的。
函数 f(x) 在 x=0 处的左极限为 $\lim _{x\rightarrow 0^{-}}f(x)=\lim _{x\rightarrow 0^{-}}{e}^{\dfrac {1}{x}}$,右极限为 $\lim _{x\rightarrow 0^{+}}f(x)=\lim _{x\rightarrow 0^{+}}\ln (1+x)$。
步骤 2:计算左极限
当 x 趋近于 0 的左侧时,$\dfrac {1}{x}$ 趋近于负无穷大,因此 ${e}^{\dfrac {1}{x}}$ 趋近于 0。所以,$\lim _{x\rightarrow 0^{-}}f(x)=0$。
步骤 3:计算右极限
当 x 趋近于 0 的右侧时,$\ln (1+x)$ 趋近于 $\ln (1+0)=\ln 1=0$。所以,$\lim _{x\rightarrow 0^{+}}f(x)=0$。
步骤 4:判断函数在 x=0 处的连续性
由于 $\lim _{x\rightarrow 0^{-}}f(x)=\lim _{x\rightarrow 0^{+}}f(x)=0$,且 f(0)=ln(1+0)=0,所以函数 f(x) 在 x=0 处是连续的。