int (e)^x(sin )^2xdx.
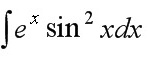 .
.
题目解答
答案
![]() ,
,
而 ![]()
![]() ,
,
![]() ,
,
所以 ![]() .
.
解析
考查要点:本题主要考查分部积分法和三角恒等式的应用,需要将被积函数中的$\sin^2 x$通过恒等式转换为更易积分的形式,再结合分部积分完成计算。
解题核心思路:
- 利用三角恒等式将$\sin^2 x$转化为$\frac{1 - \cos 2x}{2}$,简化积分形式;
- 拆分积分为两个更简单的积分之和;
- 对含$\cos 2x$的积分使用分部积分法,通过两次分部积分构造方程求解。
破题关键点:
- 正确应用三角恒等式是简化积分的关键;
- 分部积分法的两次应用需注意符号和系数的处理,避免计算错误。
步骤1:应用三角恒等式
利用$\sin^2 x = \frac{1 - \cos 2x}{2}$,原积分变为:
$\int e^x \sin^2 x \, dx = \frac{1}{2} \int e^x (1 - \cos 2x) \, dx = \frac{1}{2} \int e^x \, dx - \frac{1}{2} \int e^x \cos 2x \, dx$
步骤2:计算第一个积分
直接积分$\int e^x \, dx$:
$\frac{1}{2} \int e^x \, dx = \frac{1}{2} e^x$
步骤3:处理第二个积分$\int e^x \cos 2x \, dx$
第一次分部积分:
设$u = \cos 2x$,$dv = e^x dx$,则$du = -2 \sin 2x dx$,$v = e^x$:
$\int e^x \cos 2x \, dx = e^x \cos 2x + 2 \int e^x \sin 2x \, dx$
第二次分部积分:
对$\int e^x \sin 2x \, dx$,设$u = \sin 2x$,$dv = e^x dx$,则$du = 2 \cos 2x dx$,$v = e^x$:
$\int e^x \sin 2x \, dx = e^x \sin 2x - 2 \int e^x \cos 2x \, dx$
构造方程:
将第二次分部积分的结果代入第一次的结果:
$\int e^x \cos 2x \, dx = e^x \cos 2x + 2 \left( e^x \sin 2x - 2 \int e^x \cos 2x \, dx \right)$
整理得:
$\int e^x \cos 2x \, dx = \frac{e^x}{5} (\cos 2x + 2 \sin 2x) + C$
步骤4:合并所有结果
将$\int e^x \cos 2x \, dx$代入原积分表达式:
$\int e^x \sin^2 x \, dx = \frac{1}{2} e^x - \frac{1}{10} e^x (\cos 2x + 2 \sin 2x) + C$