题目
(12)曲线 =dfrac (x+4sin x)(5x-2cos x) 的水平渐近线方程为 __
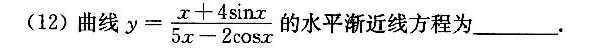
题目解答
答案
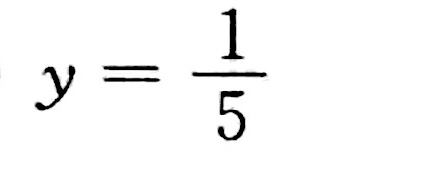
解析
步骤 1:确定水平渐近线的定义
水平渐近线是指当 $x$ 趋向于正无穷或负无穷时,函数 $y$ 趋向于某个常数值。对于有理函数,水平渐近线的确定通常依赖于分子和分母的最高次项的系数比。
步骤 2:分析函数的极限
对于函数 $y=\dfrac {x+4\sin x}{5x-2\cos x}$,当 $x$ 趋向于正无穷或负无穷时,$\sin x$ 和 $\cos x$ 的值在 $[-1, 1]$ 之间波动,因此它们对分子和分母的主导项没有影响。因此,我们主要关注 $x$ 的最高次项。
步骤 3:计算极限
计算极限 $\lim_{x \to \infty} \dfrac {x+4\sin x}{5x-2\cos x}$,可以将分子和分母同时除以 $x$,得到:
$$\lim_{x \to \infty} \dfrac {1+\frac{4\sin x}{x}}{5-\frac{2\cos x}{x}}$$
由于 $\lim_{x \to \infty} \frac{\sin x}{x} = 0$ 和 $\lim_{x \to \infty} \frac{\cos x}{x} = 0$,因此极限简化为:
$$\lim_{x \to \infty} \dfrac {1+0}{5-0} = \dfrac {1}{5}$$
水平渐近线是指当 $x$ 趋向于正无穷或负无穷时,函数 $y$ 趋向于某个常数值。对于有理函数,水平渐近线的确定通常依赖于分子和分母的最高次项的系数比。
步骤 2:分析函数的极限
对于函数 $y=\dfrac {x+4\sin x}{5x-2\cos x}$,当 $x$ 趋向于正无穷或负无穷时,$\sin x$ 和 $\cos x$ 的值在 $[-1, 1]$ 之间波动,因此它们对分子和分母的主导项没有影响。因此,我们主要关注 $x$ 的最高次项。
步骤 3:计算极限
计算极限 $\lim_{x \to \infty} \dfrac {x+4\sin x}{5x-2\cos x}$,可以将分子和分母同时除以 $x$,得到:
$$\lim_{x \to \infty} \dfrac {1+\frac{4\sin x}{x}}{5-\frac{2\cos x}{x}}$$
由于 $\lim_{x \to \infty} \frac{\sin x}{x} = 0$ 和 $\lim_{x \to \infty} \frac{\cos x}{x} = 0$,因此极限简化为:
$$\lim_{x \to \infty} \dfrac {1+0}{5-0} = \dfrac {1}{5}$$