题目
(1),求,,.(2),分别求.(3),分别求.
(1)
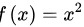 ,求
,求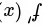 ,
,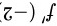 ,
,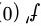 .
.
(2)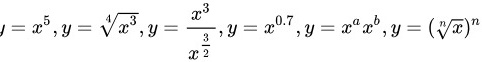 ,分别求
,分别求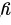 .
.
(3)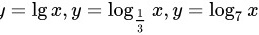 ,分别求
,分别求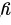 .
.
题目解答
答案
(1)
∵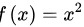
∴一阶导数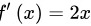
∴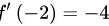 ,
,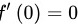 .
.
(2)
根据幂级数的求导公式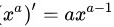 可得:
可得:
对于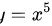 ,
,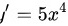 ,
,
对于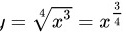 ,
,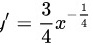
对于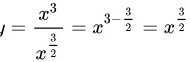 ,
,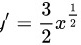
对于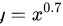 ,
,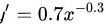
对于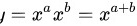 ,
,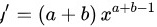
对于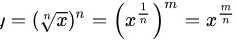 ,
,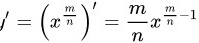
(3)
根据求导公式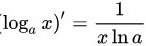 可得:
可得:
对于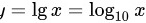 ,
,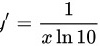
对于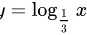 ,
,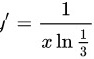
对于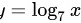 ,
,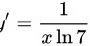 .
.
解析
步骤 1:求f'(x)
根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$f(x)={x}^{2}$求导,得到$f'(x)=2x$。
步骤 2:求f'(-2)
将x=-2代入$f'(x)=2x$,得到$f'(-2)=2(-2)=-4$。
步骤 3:求f(0)
将x=0代入$f(x)={x}^{2}$,得到$f(0)={0}^{2}=0$。
【答案】
$f'(x)=2x$,$f'(-2)=-4$,$f(0)=0$。
(2)
$y={x}^{5}$,$y=\sqrt [4]{{x}^{3}}$,$y=\dfrac {{x}^{3}}{{x}^{\dfrac {3}{2}}}$,$y={x}^{0.7}$,$y={x}^{a}{x}^{b}$,$y={(\sqrt [n]{x})}^{n}$,分别求导。
【解析】
步骤 1:求$y={x}^{5}$的导数
根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{5}$求导,得到$y'=5{x}^{4}$。
步骤 2:求$y=\sqrt [4]{{x}^{3}}$的导数
将$y=\sqrt [4]{{x}^{3}}$写成$y={x}^{\dfrac {3}{4}}$,根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{\dfrac {3}{4}}$求导,得到$y'=\dfrac {3}{4}{x}^{-\dfrac {1}{4}}$。
步骤 3:求$y=\dfrac {{x}^{3}}{{x}^{\dfrac {3}{2}}}$的导数
将$y=\dfrac {{x}^{3}}{{x}^{\dfrac {3}{2}}}$写成$y={x}^{3-\dfrac {3}{2}}={x}^{\dfrac {3}{2}}$,根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{\dfrac {3}{2}}$求导,得到$y'=\dfrac {3}{2}{x}^{\dfrac {1}{2}}$。
步骤 4:求$y={x}^{0.7}$的导数
根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{0.7}$求导,得到$y'=0.7{x}^{-0.3}$。
步骤 5:求$y={x}^{a}{x}^{b}$的导数
将$y={x}^{a}{x}^{b}$写成$y={x}^{a+b}$,根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{a+b}$求导,得到$y'=(a+b){x}^{a+b-1}$。
步骤 6:求$y={(\sqrt [n]{x})}^{n}$的导数
将$y={(\sqrt [n]{x})}^{n}$写成$y={x}^{\dfrac {n}{n}}={x}^{1}$,根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{1}$求导,得到$y'=1{x}^{0}=1$。
根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$f(x)={x}^{2}$求导,得到$f'(x)=2x$。
步骤 2:求f'(-2)
将x=-2代入$f'(x)=2x$,得到$f'(-2)=2(-2)=-4$。
步骤 3:求f(0)
将x=0代入$f(x)={x}^{2}$,得到$f(0)={0}^{2}=0$。
【答案】
$f'(x)=2x$,$f'(-2)=-4$,$f(0)=0$。
(2)
$y={x}^{5}$,$y=\sqrt [4]{{x}^{3}}$,$y=\dfrac {{x}^{3}}{{x}^{\dfrac {3}{2}}}$,$y={x}^{0.7}$,$y={x}^{a}{x}^{b}$,$y={(\sqrt [n]{x})}^{n}$,分别求导。
【解析】
步骤 1:求$y={x}^{5}$的导数
根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{5}$求导,得到$y'=5{x}^{4}$。
步骤 2:求$y=\sqrt [4]{{x}^{3}}$的导数
将$y=\sqrt [4]{{x}^{3}}$写成$y={x}^{\dfrac {3}{4}}$,根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{\dfrac {3}{4}}$求导,得到$y'=\dfrac {3}{4}{x}^{-\dfrac {1}{4}}$。
步骤 3:求$y=\dfrac {{x}^{3}}{{x}^{\dfrac {3}{2}}}$的导数
将$y=\dfrac {{x}^{3}}{{x}^{\dfrac {3}{2}}}$写成$y={x}^{3-\dfrac {3}{2}}={x}^{\dfrac {3}{2}}$,根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{\dfrac {3}{2}}$求导,得到$y'=\dfrac {3}{2}{x}^{\dfrac {1}{2}}$。
步骤 4:求$y={x}^{0.7}$的导数
根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{0.7}$求导,得到$y'=0.7{x}^{-0.3}$。
步骤 5:求$y={x}^{a}{x}^{b}$的导数
将$y={x}^{a}{x}^{b}$写成$y={x}^{a+b}$,根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{a+b}$求导,得到$y'=(a+b){x}^{a+b-1}$。
步骤 6:求$y={(\sqrt [n]{x})}^{n}$的导数
将$y={(\sqrt [n]{x})}^{n}$写成$y={x}^{\dfrac {n}{n}}={x}^{1}$,根据幂函数的求导公式${x}^{n})'=n{x}^{n-1}$,对$y={x}^{1}$求导,得到$y'=1{x}^{0}=1$。