题目
(19) =ln ((e)^x+sqrt (1+{e)^2x}).
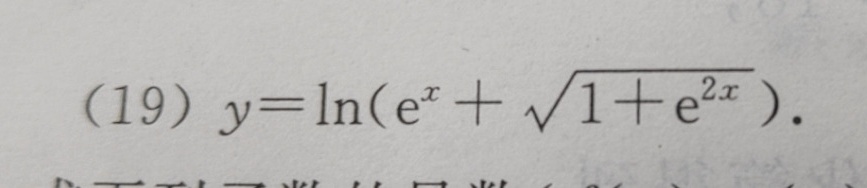
题目解答
答案
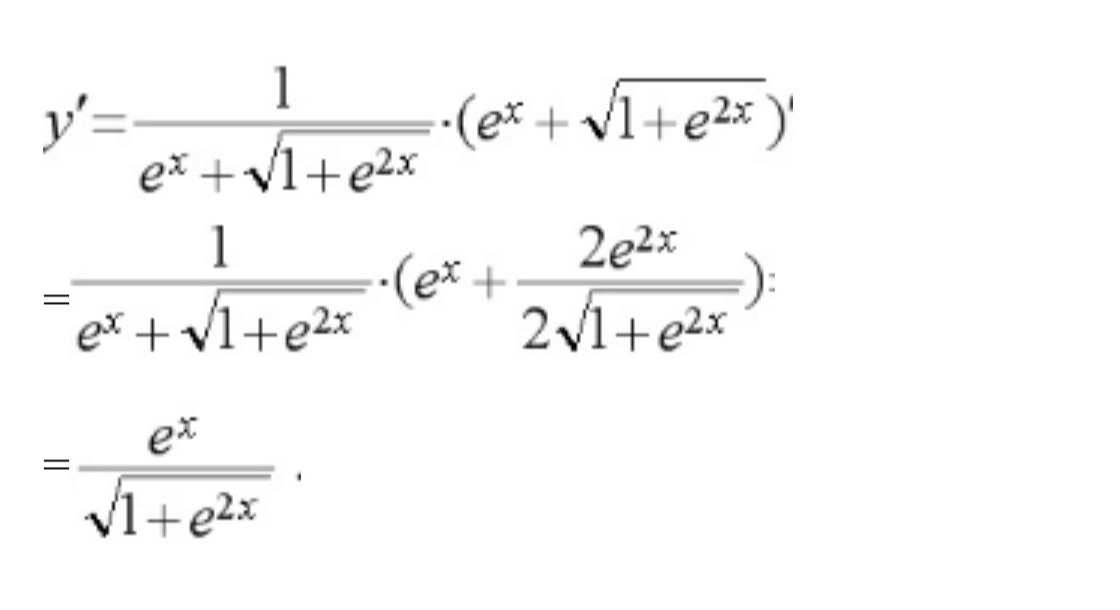
解析
步骤 1:求导数
根据链式法则,对函数 $y=\ln ({e}^{x}+\sqrt {1+{e}^{2x}})$ 求导,首先需要对内部函数 ${e}^{x}+\sqrt {1+{e}^{2x}}$ 求导。
步骤 2:计算内部函数的导数
内部函数的导数为 ${e}^{x}+\dfrac{1}{2}\cdot(1+{e}^{2x})^{-\frac{1}{2}}\cdot2{e}^{2x}={e}^{x}+\dfrac{{e}^{2x}}{\sqrt{1+{e}^{2x}}}$。
步骤 3:应用链式法则
将内部函数的导数代入链式法则,得到 $y'=\dfrac{1}{{e}^{x}+\sqrt{1+{e}^{2x}}}\cdot({e}^{x}+\dfrac{{e}^{2x}}{\sqrt{1+{e}^{2x}}})$。
步骤 4:化简
化简得到 $y'=\dfrac{{e}^{x}}{\sqrt{1+{e}^{2x}}}$。
根据链式法则,对函数 $y=\ln ({e}^{x}+\sqrt {1+{e}^{2x}})$ 求导,首先需要对内部函数 ${e}^{x}+\sqrt {1+{e}^{2x}}$ 求导。
步骤 2:计算内部函数的导数
内部函数的导数为 ${e}^{x}+\dfrac{1}{2}\cdot(1+{e}^{2x})^{-\frac{1}{2}}\cdot2{e}^{2x}={e}^{x}+\dfrac{{e}^{2x}}{\sqrt{1+{e}^{2x}}}$。
步骤 3:应用链式法则
将内部函数的导数代入链式法则,得到 $y'=\dfrac{1}{{e}^{x}+\sqrt{1+{e}^{2x}}}\cdot({e}^{x}+\dfrac{{e}^{2x}}{\sqrt{1+{e}^{2x}}})$。
步骤 4:化简
化简得到 $y'=\dfrac{{e}^{x}}{\sqrt{1+{e}^{2x}}}$。