利用洛必达法则求极限.-|||-lim _(xarrow {0)^+}((cos sqrt {x))}^dfrac (pi {x)}

题目解答
答案
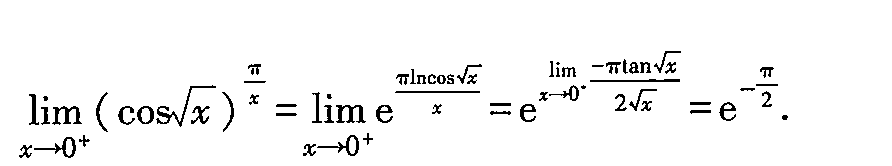
解析
考查要点:本题主要考查利用洛必达法则求解形如$1^{\infty}$型未定式极限的能力,以及对自然对数与指数函数转换的理解。
解题核心思路:
- 识别极限类型:当$x \to 0^+$时,$\cos \sqrt{x} \to 1$,而指数$\dfrac{\pi}{x} \to +\infty$,属于$1^{\infty}$型未定式。
- 转换形式:通过取自然对数将原式转化为指数函数形式,将问题转化为求指数部分的极限。
- 应用洛必达法则:对转换后的极限表达式应用洛必达法则,化简后求得最终结果。
破题关键点:
- 正确应用对数转换,将原式转化为$\exp\left(\lim \dfrac{\ln(\cos \sqrt{x})}{x/\pi}\right)$。
- 识别$0/0$型未定式,对分子分母分别求导,通过洛必达法则化简极限。
设原式为$L = \lim _{x\rightarrow {0}^{+}}{(\cos \sqrt {x})}^{\dfrac {\pi }{x}}$,步骤如下:
步骤1:取自然对数
对$L$取自然对数:
$\ln L = \lim _{x\rightarrow 0^{+}} \dfrac{\pi}{x} \cdot \ln(\cos \sqrt{x}).$
步骤2:转换为$0/0$型
将表达式改写为:
$\ln L = \lim _{x\rightarrow 0^{+}} \dfrac{\ln(\cos \sqrt{x})}{x/\pi}.$
当$x \to 0^+$时,分子$\ln(\cos \sqrt{x}) \to 0$,分母$x/\pi \to 0$,属于$0/0$型未定式,可应用洛必达法则。
步骤3:应用洛必达法则
对分子和分母分别求导:
- 分子导数:
$\dfrac{d}{dx} \ln(\cos \sqrt{x}) = \dfrac{1}{\cos \sqrt{x}} \cdot (-\sin \sqrt{x}) \cdot \dfrac{1}{2\sqrt{x}} = -\dfrac{\sin \sqrt{x}}{2\sqrt{x} \cos \sqrt{x}}.$ - 分母导数:
$\dfrac{d}{dx} \left( \dfrac{x}{\pi} \right) = \dfrac{1}{\pi}.$
步骤4:化简极限
代入洛必达法则结果:
$\ln L = \lim _{x\rightarrow 0^{+}} \dfrac{ -\dfrac{\sin \sqrt{x}}{2\sqrt{x} \cos \sqrt{x}} }{ \dfrac{1}{\pi} } = \lim _{x\rightarrow 0^{+}} -\dfrac{\pi \sin \sqrt{x}}{2\sqrt{x} \cos \sqrt{x}}.$
步骤5:利用等价无穷小
当$x \to 0^+$时,$\sin \sqrt{x} \approx \sqrt{x}$,$\cos \sqrt{x} \approx 1$,代入得:
$\ln L = \lim _{x\rightarrow 0^{+}} -\dfrac{\pi \cdot \sqrt{x}}{2\sqrt{x} \cdot 1} = -\dfrac{\pi}{2}.$
步骤6:还原指数形式
因此,原式极限为:
$L = e^{\ln L} = e^{-\pi/2}.$