题目
(9)lim _(xarrow 0)dfrac (sqrt {1+5x)-sqrt (1-3x)}({x)^2+2x} .
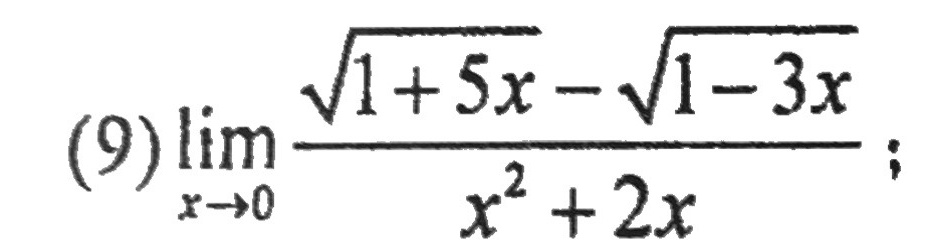
题目解答
答案
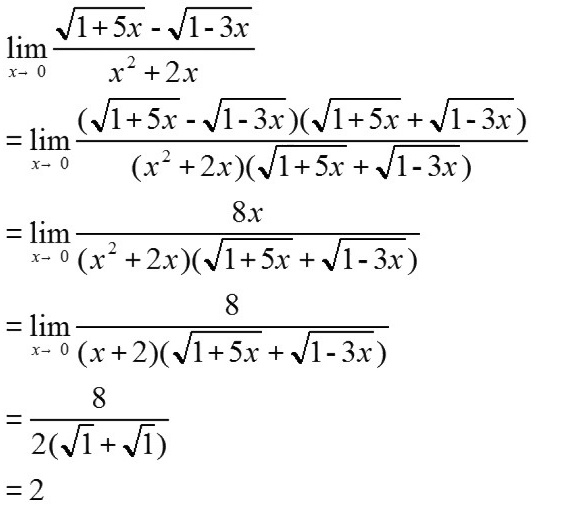
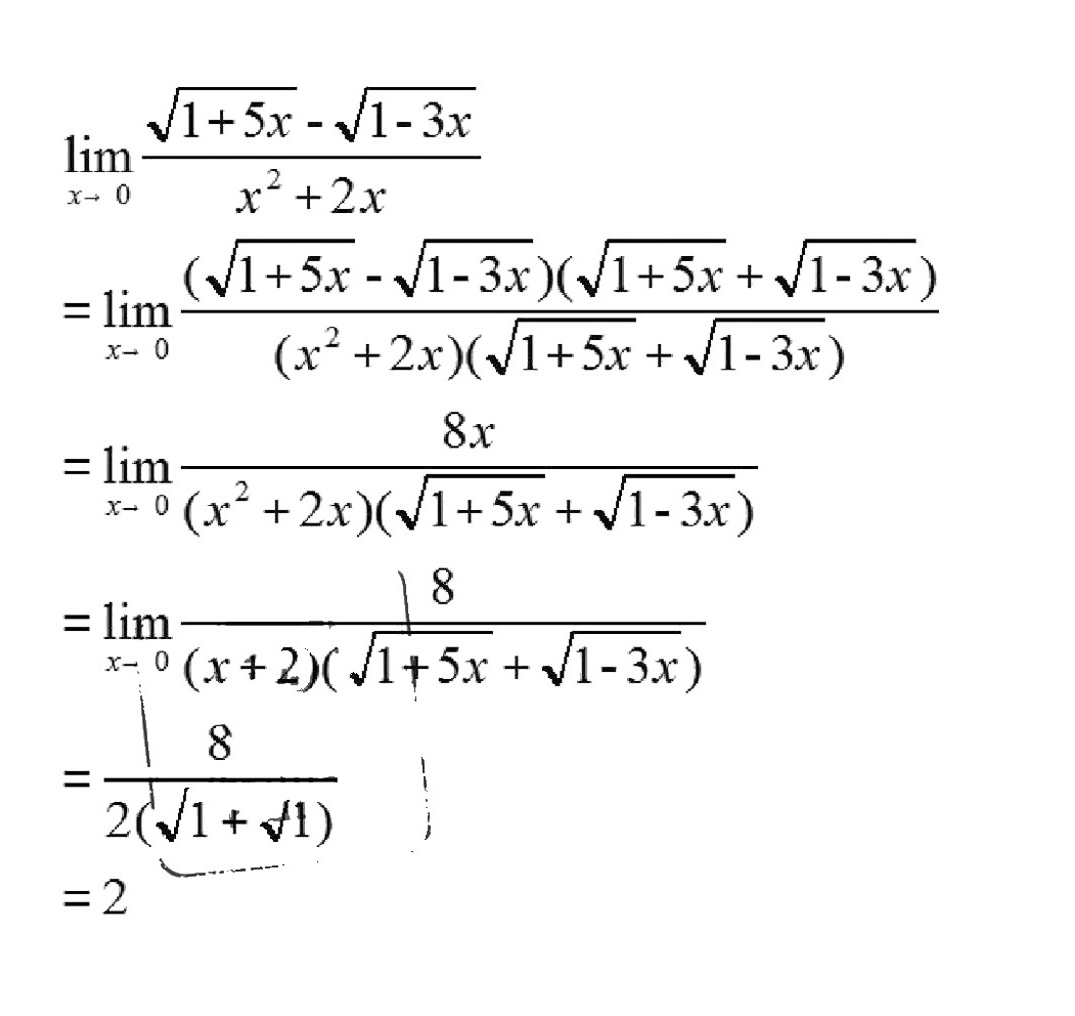
解析
步骤 1:有理化分子
为了消除分子中的根号,我们使用有理化的方法,即乘以分子和分母的共轭式。分子的共轭式为 $\sqrt{1+5x} + \sqrt{1-3x}$。因此,我们有:
$$\lim _{x\rightarrow 0}\dfrac {\sqrt {1+5x}-\sqrt {1-3x}}{{x}^{2}+2x} = \lim _{x\rightarrow 0}\dfrac {(\sqrt {1+5x}-\sqrt {1-3x})(\sqrt {1+5x}+\sqrt {1-3x})}{({x}^{2}+2x)(\sqrt {1+5x}+\sqrt {1-3x})}$$
步骤 2:化简分子
分子中的根号相乘后,可以化简为:
$$\lim _{x\rightarrow 0}\dfrac {8x}{({x}^{2}+2x)(\sqrt {1+5x}+\sqrt {1-3x})}$$
步骤 3:化简分母
将分母中的 $x^2 + 2x$ 提取公因数 $x$,得到:
$$\lim _{x\rightarrow 0}\dfrac {8}{(x+2)(\sqrt {1+5x}+\sqrt {1-3x})}$$
步骤 4:代入 $x=0$
将 $x=0$ 代入上式,得到:
$$\dfrac {8}{2(\sqrt {1}+\sqrt {1})} = \dfrac {8}{2(1+1)} = \dfrac {8}{4} = 2$$
为了消除分子中的根号,我们使用有理化的方法,即乘以分子和分母的共轭式。分子的共轭式为 $\sqrt{1+5x} + \sqrt{1-3x}$。因此,我们有:
$$\lim _{x\rightarrow 0}\dfrac {\sqrt {1+5x}-\sqrt {1-3x}}{{x}^{2}+2x} = \lim _{x\rightarrow 0}\dfrac {(\sqrt {1+5x}-\sqrt {1-3x})(\sqrt {1+5x}+\sqrt {1-3x})}{({x}^{2}+2x)(\sqrt {1+5x}+\sqrt {1-3x})}$$
步骤 2:化简分子
分子中的根号相乘后,可以化简为:
$$\lim _{x\rightarrow 0}\dfrac {8x}{({x}^{2}+2x)(\sqrt {1+5x}+\sqrt {1-3x})}$$
步骤 3:化简分母
将分母中的 $x^2 + 2x$ 提取公因数 $x$,得到:
$$\lim _{x\rightarrow 0}\dfrac {8}{(x+2)(\sqrt {1+5x}+\sqrt {1-3x})}$$
步骤 4:代入 $x=0$
将 $x=0$ 代入上式,得到:
$$\dfrac {8}{2(\sqrt {1}+\sqrt {1})} = \dfrac {8}{2(1+1)} = \dfrac {8}{4} = 2$$