题目
计算下列极限 (1) lim _(xarrow 0)((1-2{x)^2)}dfrac (1)(xsin x)-|||-__(1) lim _(xarrow 0)((1-2{x)^2)}dfrac (1)(xsin x)-|||-__(1) lim _(xarrow 0)((1-2{x)^2)}dfrac (1)(xsin x)-|||-__(1) lim _(xarrow 0)((1-2{x)^2)}dfrac (1)(xsin x)-|||-__
计算下列极限
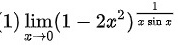
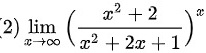
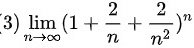
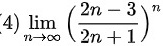
题目解答
答案
解: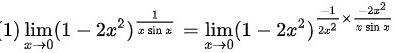
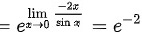
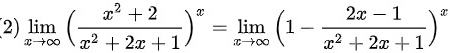
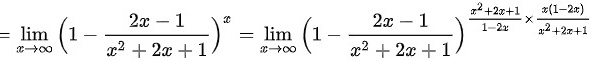
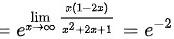

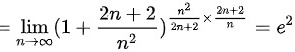
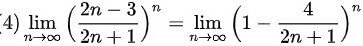
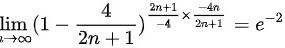
解析
步骤 1:计算(1)的极限
$\lim _{x\rightarrow 0}(1-2{x}^{2})\dfrac {1}{x\sin x}$
$=\lim _{x\rightarrow 0}(1-2{x}^{2})$
$={e}^{x\rightarrow 0}\dfrac {-2x}{\sin x}$
$={e}^{-2}$
步骤 2:计算(2)的极限
$\lim _{x\rightarrow \infty }{(\dfrac {{x}^{2}+2}{{x}^{2}+2x+1})}^{x}$
$=\lim _{x\rightarrow \infty }(1-\dfrac {2x-1}{{x}^{2}+2x+1})^{x}$
$=\lim _{x\rightarrow +\infty }(1-\dfrac {2x-1}{{x}^{2}+2x+1})^{x}$
$={e}^{x+\infty }\dfrac {\alpha (1-2x)}{{x}^{2}+2x+1}$
$={e}^{-2}$
步骤 3:计算(3)的极限
$\lim _{n\rightarrow \infty }{(1+\dfrac {2}{n}+\dfrac {2}{{n}^{2}})}^{n}$
$=\lim _{n\rightarrow \infty }{(1+\dfrac {2n+2}{{n}^{2}})}^{n}$
$=\lim _{n\rightarrow \infty }{(1+\dfrac {2n+2}{{n}^{2}})}^{\dfrac {{n}^{2}}{2n+2}}\times \dfrac {2n+2}{n}$
$={e}^{2}$
步骤 4:计算(4)的极限
$\lim _{n\rightarrow \infty }{(\dfrac {2n-3}{2n+1})}^{n}$
$=\lim _{n\rightarrow \infty }{(1-\dfrac {4}{2n+1})}^{n}$
$=\lim _{n\rightarrow \infty }{(1-\dfrac {4}{2n+1})}^{\dfrac {2n+1}{-4}}\times \dfrac {-4n}{2n+1}$
$={e}^{-2}$
$\lim _{x\rightarrow 0}(1-2{x}^{2})\dfrac {1}{x\sin x}$
$=\lim _{x\rightarrow 0}(1-2{x}^{2})$
$={e}^{x\rightarrow 0}\dfrac {-2x}{\sin x}$
$={e}^{-2}$
步骤 2:计算(2)的极限
$\lim _{x\rightarrow \infty }{(\dfrac {{x}^{2}+2}{{x}^{2}+2x+1})}^{x}$
$=\lim _{x\rightarrow \infty }(1-\dfrac {2x-1}{{x}^{2}+2x+1})^{x}$
$=\lim _{x\rightarrow +\infty }(1-\dfrac {2x-1}{{x}^{2}+2x+1})^{x}$
$={e}^{x+\infty }\dfrac {\alpha (1-2x)}{{x}^{2}+2x+1}$
$={e}^{-2}$
步骤 3:计算(3)的极限
$\lim _{n\rightarrow \infty }{(1+\dfrac {2}{n}+\dfrac {2}{{n}^{2}})}^{n}$
$=\lim _{n\rightarrow \infty }{(1+\dfrac {2n+2}{{n}^{2}})}^{n}$
$=\lim _{n\rightarrow \infty }{(1+\dfrac {2n+2}{{n}^{2}})}^{\dfrac {{n}^{2}}{2n+2}}\times \dfrac {2n+2}{n}$
$={e}^{2}$
步骤 4:计算(4)的极限
$\lim _{n\rightarrow \infty }{(\dfrac {2n-3}{2n+1})}^{n}$
$=\lim _{n\rightarrow \infty }{(1-\dfrac {4}{2n+1})}^{n}$
$=\lim _{n\rightarrow \infty }{(1-\dfrac {4}{2n+1})}^{\dfrac {2n+1}{-4}}\times \dfrac {-4n}{2n+1}$
$={e}^{-2}$