题目
11.设 (x)=dfrac (x)(sqrt {1+{x)^2}} 求 [ f(x)] , f[ f(x)] .
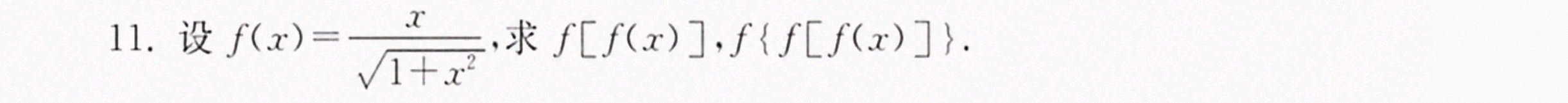
题目解答
答案
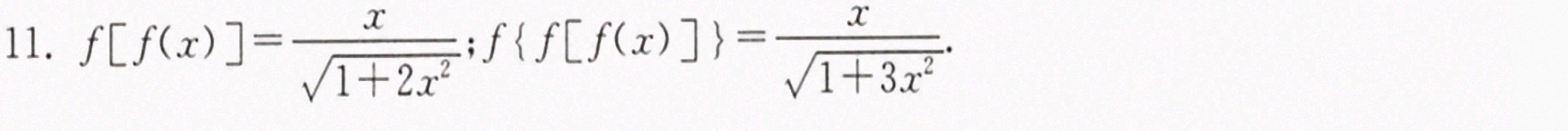
解析
步骤 1:计算 $f[f(x)]$
首先,我们已知 $f(x)=\dfrac {x}{\sqrt {1+{x}^{2}}}$。为了计算 $f[f(x)]$,我们需要将 $f(x)$ 代入 $f$ 的定义中。即,将 $f(x)$ 的表达式代入 $x$ 的位置。
$$f[f(x)] = f\left(\dfrac {x}{\sqrt {1+{x}^{2}}}\right) = \dfrac {\dfrac {x}{\sqrt {1+{x}^{2}}}}{\sqrt {1+\left(\dfrac {x}{\sqrt {1+{x}^{2}}}\right)^2}}$$
步骤 2:化简 $f[f(x)]$
化简上述表达式,我们得到:
$$f[f(x)] = \dfrac {\dfrac {x}{\sqrt {1+{x}^{2}}}}{\sqrt {1+\dfrac {x^2}{1+{x}^{2}}}} = \dfrac {\dfrac {x}{\sqrt {1+{x}^{2}}}}{\sqrt {\dfrac {1+{x}^{2}+x^2}{1+{x}^{2}}}} = \dfrac {\dfrac {x}{\sqrt {1+{x}^{2}}}}{\sqrt {\dfrac {1+2{x}^{2}}{1+{x}^{2}}}} = \dfrac {x}{\sqrt {1+2{x}^{2}}}$$
步骤 3:计算 $f\{ f[ f(x)] \}$
接下来,我们计算 $f\{ f[ f(x)] \}$,即 $f\left(\dfrac {x}{\sqrt {1+2{x}^{2}}}\right)$。
$$f\{ f[ f(x)] \} = f\left(\dfrac {x}{\sqrt {1+2{x}^{2}}}\right) = \dfrac {\dfrac {x}{\sqrt {1+2{x}^{2}}}}{\sqrt {1+\left(\dfrac {x}{\sqrt {1+2{x}^{2}}}\right)^2}}$$
步骤 4:化简 $f\{ f[ f(x)] \}$
化简上述表达式,我们得到:
$$f\{ f[ f(x)] \} = \dfrac {\dfrac {x}{\sqrt {1+2{x}^{2}}}}{\sqrt {1+\dfrac {x^2}{1+2{x}^{2}}}} = \dfrac {\dfrac {x}{\sqrt {1+2{x}^{2}}}}{\sqrt {\dfrac {1+2{x}^{2}+x^2}{1+2{x}^{2}}}} = \dfrac {\dfrac {x}{\sqrt {1+2{x}^{2}}}}{\sqrt {\dfrac {1+3{x}^{2}}{1+2{x}^{2}}}} = \dfrac {x}{\sqrt {1+3{x}^{2}}}$$
首先,我们已知 $f(x)=\dfrac {x}{\sqrt {1+{x}^{2}}}$。为了计算 $f[f(x)]$,我们需要将 $f(x)$ 代入 $f$ 的定义中。即,将 $f(x)$ 的表达式代入 $x$ 的位置。
$$f[f(x)] = f\left(\dfrac {x}{\sqrt {1+{x}^{2}}}\right) = \dfrac {\dfrac {x}{\sqrt {1+{x}^{2}}}}{\sqrt {1+\left(\dfrac {x}{\sqrt {1+{x}^{2}}}\right)^2}}$$
步骤 2:化简 $f[f(x)]$
化简上述表达式,我们得到:
$$f[f(x)] = \dfrac {\dfrac {x}{\sqrt {1+{x}^{2}}}}{\sqrt {1+\dfrac {x^2}{1+{x}^{2}}}} = \dfrac {\dfrac {x}{\sqrt {1+{x}^{2}}}}{\sqrt {\dfrac {1+{x}^{2}+x^2}{1+{x}^{2}}}} = \dfrac {\dfrac {x}{\sqrt {1+{x}^{2}}}}{\sqrt {\dfrac {1+2{x}^{2}}{1+{x}^{2}}}} = \dfrac {x}{\sqrt {1+2{x}^{2}}}$$
步骤 3:计算 $f\{ f[ f(x)] \}$
接下来,我们计算 $f\{ f[ f(x)] \}$,即 $f\left(\dfrac {x}{\sqrt {1+2{x}^{2}}}\right)$。
$$f\{ f[ f(x)] \} = f\left(\dfrac {x}{\sqrt {1+2{x}^{2}}}\right) = \dfrac {\dfrac {x}{\sqrt {1+2{x}^{2}}}}{\sqrt {1+\left(\dfrac {x}{\sqrt {1+2{x}^{2}}}\right)^2}}$$
步骤 4:化简 $f\{ f[ f(x)] \}$
化简上述表达式,我们得到:
$$f\{ f[ f(x)] \} = \dfrac {\dfrac {x}{\sqrt {1+2{x}^{2}}}}{\sqrt {1+\dfrac {x^2}{1+2{x}^{2}}}} = \dfrac {\dfrac {x}{\sqrt {1+2{x}^{2}}}}{\sqrt {\dfrac {1+2{x}^{2}+x^2}{1+2{x}^{2}}}} = \dfrac {\dfrac {x}{\sqrt {1+2{x}^{2}}}}{\sqrt {\dfrac {1+3{x}^{2}}{1+2{x}^{2}}}} = \dfrac {x}{\sqrt {1+3{x}^{2}}}$$