题目
5.lim _(narrow infty )((dfrac {2n-3)(2n+1))}^n
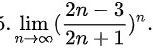
题目解答
答案
解答过程如下:
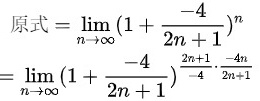
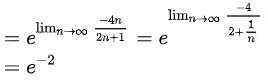
解析
步骤 1:将问题转化为指数形式
将给定的极限问题转化为指数形式,以便于使用自然对数和指数函数的性质进行求解。
$$\lim _{n\rightarrow \infty }{(\dfrac {2n-3}{2n+1})}^{n} = \lim _{n\rightarrow \infty }{e}^{n\ln(\dfrac {2n-3}{2n+1})}$$
步骤 2:计算对数部分的极限
计算对数部分的极限,以便于进一步简化问题。
$$\lim _{n\rightarrow \infty }n\ln(\dfrac {2n-3}{2n+1}) = \lim _{n\rightarrow \infty }n\ln(\dfrac {2n-3}{2n+1}) = \lim _{n\rightarrow \infty }n\ln(1-\dfrac {4}{2n+1})$$
$$= \lim _{n\rightarrow \infty }n(-\dfrac {4}{2n+1}) = \lim _{n\rightarrow \infty }-\dfrac {4n}{2n+1} = -2$$
步骤 3:计算最终的极限
将对数部分的极限结果代入指数形式,计算最终的极限。
$$\lim _{n\rightarrow \infty }{e}^{n\ln(\dfrac {2n-3}{2n+1})} = {e}^{-2}$$
将给定的极限问题转化为指数形式,以便于使用自然对数和指数函数的性质进行求解。
$$\lim _{n\rightarrow \infty }{(\dfrac {2n-3}{2n+1})}^{n} = \lim _{n\rightarrow \infty }{e}^{n\ln(\dfrac {2n-3}{2n+1})}$$
步骤 2:计算对数部分的极限
计算对数部分的极限,以便于进一步简化问题。
$$\lim _{n\rightarrow \infty }n\ln(\dfrac {2n-3}{2n+1}) = \lim _{n\rightarrow \infty }n\ln(\dfrac {2n-3}{2n+1}) = \lim _{n\rightarrow \infty }n\ln(1-\dfrac {4}{2n+1})$$
$$= \lim _{n\rightarrow \infty }n(-\dfrac {4}{2n+1}) = \lim _{n\rightarrow \infty }-\dfrac {4n}{2n+1} = -2$$
步骤 3:计算最终的极限
将对数部分的极限结果代入指数形式,计算最终的极限。
$$\lim _{n\rightarrow \infty }{e}^{n\ln(\dfrac {2n-3}{2n+1})} = {e}^{-2}$$