题目
(4) lim _(xarrow 0)dfrac (tan (2x+{x)^3)}(sin (x-{x)^2)};.
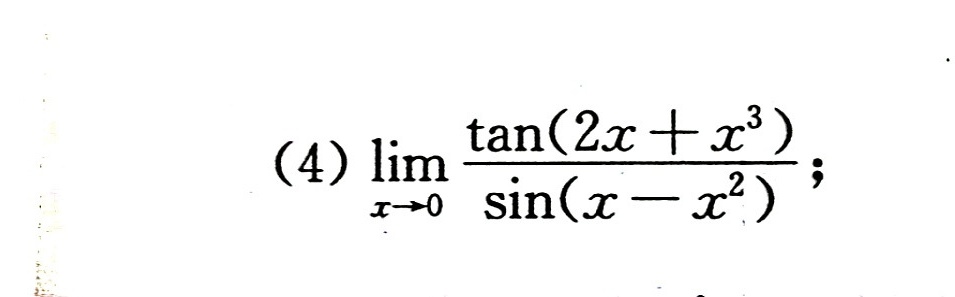 .
. 题目解答
答案
原式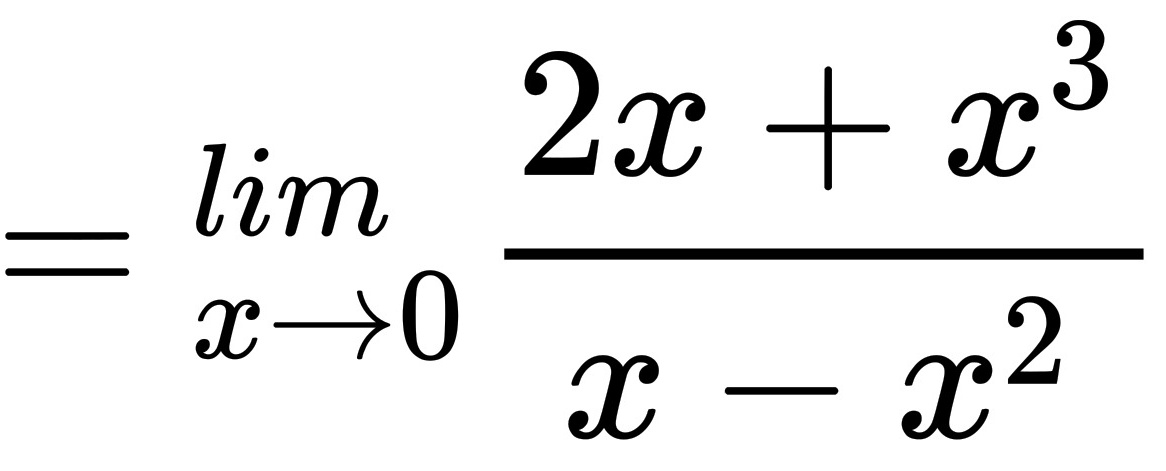
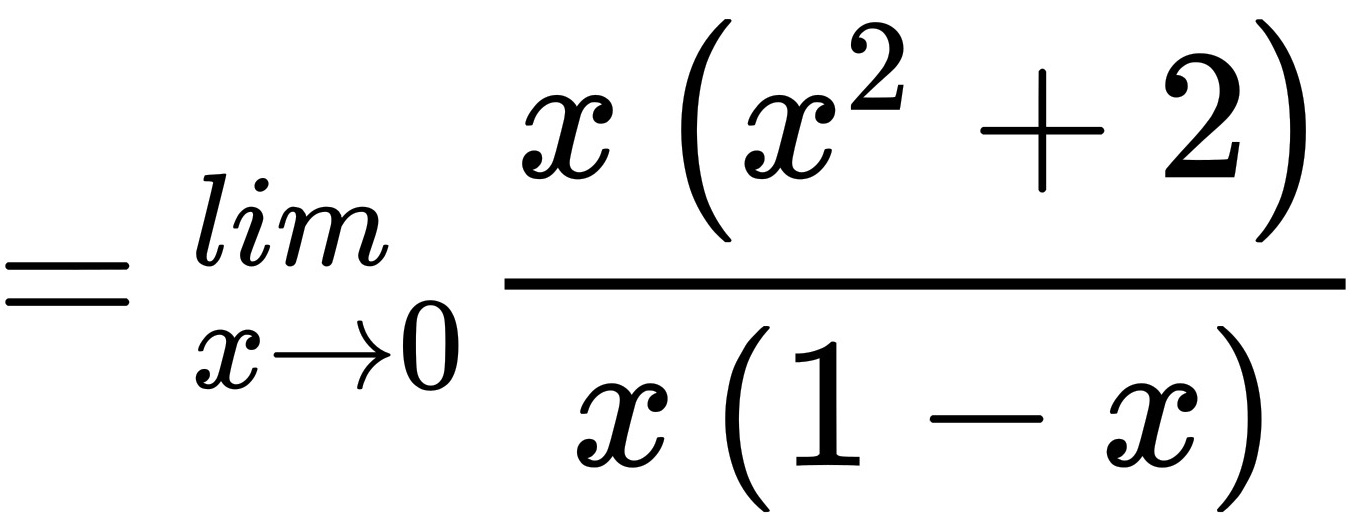
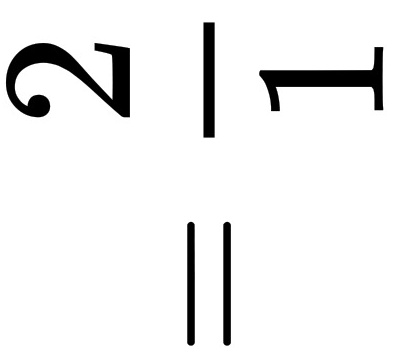
=2
.解析
步骤 1:利用等价无穷小替换
当 $x \rightarrow 0$ 时,$\tan x \sim x$ 和 $\sin x \sim x$,因此可以将 $\tan (2x+x^3)$ 替换为 $2x+x^3$,将 $\sin (x-x^2)$ 替换为 $x-x^2$。
步骤 2:代入替换后的表达式
将替换后的表达式代入原式,得到 $\lim _{x\rightarrow 0}\dfrac {2x+x^3}{x-x^2}$。
步骤 3:化简表达式
化简表达式,得到 $\lim _{x\rightarrow 0}\dfrac {2x+x^3}{x-x^2} = \lim _{x\rightarrow 0}\dfrac {x(2+x^2)}{x(1-x)} = \lim _{x\rightarrow 0}\dfrac {2+x^2}{1-x}$。
步骤 4:计算极限
计算极限,得到 $\lim _{x\rightarrow 0}\dfrac {2+x^2}{1-x} = \dfrac {2+0}{1-0} = 2$。
当 $x \rightarrow 0$ 时,$\tan x \sim x$ 和 $\sin x \sim x$,因此可以将 $\tan (2x+x^3)$ 替换为 $2x+x^3$,将 $\sin (x-x^2)$ 替换为 $x-x^2$。
步骤 2:代入替换后的表达式
将替换后的表达式代入原式,得到 $\lim _{x\rightarrow 0}\dfrac {2x+x^3}{x-x^2}$。
步骤 3:化简表达式
化简表达式,得到 $\lim _{x\rightarrow 0}\dfrac {2x+x^3}{x-x^2} = \lim _{x\rightarrow 0}\dfrac {x(2+x^2)}{x(1-x)} = \lim _{x\rightarrow 0}\dfrac {2+x^2}{1-x}$。
步骤 4:计算极限
计算极限,得到 $\lim _{x\rightarrow 0}\dfrac {2+x^2}{1-x} = \dfrac {2+0}{1-0} = 2$。