题目
(2)已知 beta =((1,-4,a))^T 可由 _(1)=((1,2,3))^T _(2)=((2,1,0))^T _(3)=((4,-1,-6))^T 线-|||-性表示,则 a= __ -
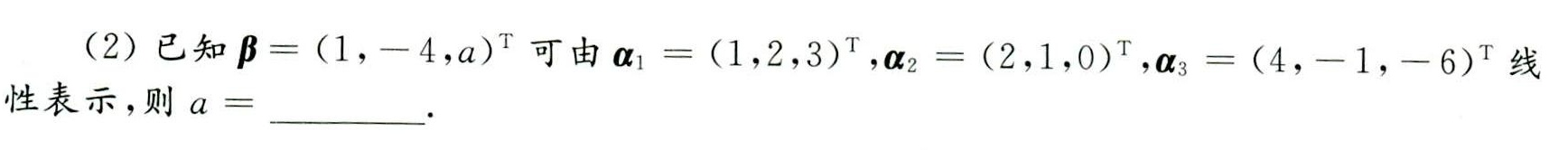
题目解答
答案
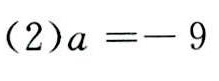
解析
步骤 1:建立线性方程组
由于 $\beta$ 可以由 ${a}_{1}$, ${a}_{2}$, ${a}_{3}$ 线性表示,因此存在实数 $x$, $y$, $z$ 使得
$$
x{a}_{1} + y{a}_{2} + z{a}_{3} = \beta
$$
即
$$
x{(1,2,3)}^{T} + y{(2,1,0)}^{T} + z{(4,-1,-6)}^{T} = {(1,-4,a)}^{T}
$$
步骤 2:将向量方程转化为线性方程组
将上述向量方程转化为线性方程组,得到
$$
\begin{cases}
x + 2y + 4z = 1 \\
2x + y - z = -4 \\
3x - 6z = a
\end{cases}
$$
步骤 3:求解线性方程组
首先解前两个方程,得到 $x$ 和 $y$ 的关系。将第一个方程乘以2,得到
$$
2x + 4y + 8z = 2
$$
将这个方程与第二个方程相减,得到
$$
3y + 9z = 6
$$
即
$$
y + 3z = 2
$$
解得
$$
y = 2 - 3z
$$
将 $y$ 的表达式代入第一个方程,得到
$$
x + 2(2 - 3z) + 4z = 1
$$
即
$$
x + 4 - 6z + 4z = 1
$$
解得
$$
x = 1 - 4 + 2z = 2z - 3
$$
将 $x$ 和 $y$ 的表达式代入第三个方程,得到
$$
3(2z - 3) - 6z = a
$$
即
$$
6z - 9 - 6z = a
$$
解得
$$
a = -9
$$
由于 $\beta$ 可以由 ${a}_{1}$, ${a}_{2}$, ${a}_{3}$ 线性表示,因此存在实数 $x$, $y$, $z$ 使得
$$
x{a}_{1} + y{a}_{2} + z{a}_{3} = \beta
$$
即
$$
x{(1,2,3)}^{T} + y{(2,1,0)}^{T} + z{(4,-1,-6)}^{T} = {(1,-4,a)}^{T}
$$
步骤 2:将向量方程转化为线性方程组
将上述向量方程转化为线性方程组,得到
$$
\begin{cases}
x + 2y + 4z = 1 \\
2x + y - z = -4 \\
3x - 6z = a
\end{cases}
$$
步骤 3:求解线性方程组
首先解前两个方程,得到 $x$ 和 $y$ 的关系。将第一个方程乘以2,得到
$$
2x + 4y + 8z = 2
$$
将这个方程与第二个方程相减,得到
$$
3y + 9z = 6
$$
即
$$
y + 3z = 2
$$
解得
$$
y = 2 - 3z
$$
将 $y$ 的表达式代入第一个方程,得到
$$
x + 2(2 - 3z) + 4z = 1
$$
即
$$
x + 4 - 6z + 4z = 1
$$
解得
$$
x = 1 - 4 + 2z = 2z - 3
$$
将 $x$ 和 $y$ 的表达式代入第三个方程,得到
$$
3(2z - 3) - 6z = a
$$
即
$$
6z - 9 - 6z = a
$$
解得
$$
a = -9
$$