题目
【多选题】下列函数为同一函数的原函数的是( )A. arctanx 和 arctanxB. arctanx和arctanxC. arctanx 和 arctanxD. arctanx和arctanx
【多选题】下列函数为同一函数的原函数的是( )
A. 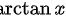 和
和 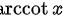
B. 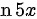 和
和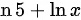
C. 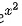 和
和 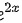
D. 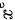 和
和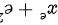
题目解答
答案
A. 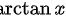 的导数为
的导数为 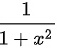 ,
,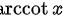 的导数为
的导数为 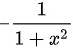 。由于两个函数的导数不相等,所以
。由于两个函数的导数不相等,所以 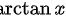 和
和 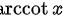 不为同一函数的原函数。
不为同一函数的原函数。
B. 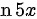 的导数为
的导数为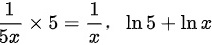 的导数为
的导数为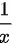 。由于两个函数的导数相等,所以
。由于两个函数的导数相等,所以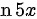 和
和 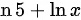 为同一函数的原函数。
为同一函数的原函数。
C.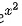 的导数为
的导数为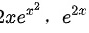 的导数为
的导数为 。由于两个函数的导数不相等,所以
。由于两个函数的导数不相等,所以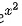 和
和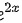 不为同一函数的原函数。
不为同一函数的原函数。
D. 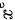 的导数为
的导数为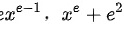 的导数为
的导数为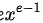 。由于两个函数的导数相等,所以
。由于两个函数的导数相等,所以 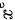 和
和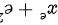 为同一函数的原函数。
为同一函数的原函数。
综上所述,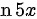 和
和 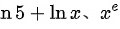 和
和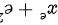 为同一函数的原函数。故选 B、D。
为同一函数的原函数。故选 B、D。
解析
步骤 1:计算arctanx的导数
arctanx的导数为 $\dfrac{1}{1+x^2}$。
步骤 2:计算arccotx的导数
arccotx的导数为 $-\dfrac{1}{1+x^2}$。
步骤 3:比较arctanx和arccotx的导数
由于arctanx和arccotx的导数不相等,所以它们不是同一函数的原函数。
步骤 4:计算n5x的导数
n5x的导数为 $\dfrac{1}{5x} \times 5 = \dfrac{1}{x}$。
步骤 5:计算$n5+\ln x$的导数
$n5+\ln x$的导数为 $\dfrac{1}{x}$。
步骤 6:比较n5x和$n5+\ln x$的导数
由于n5x和$n5+\ln x$的导数相等,所以它们是同一函数的原函数。
步骤 7:计算e^x2的导数
e^x2的导数为 $2x{e}^{{x}^{2}}$。
步骤 8:计算${2}^{2x}$的导数
${2}^{2x}$的导数为 $2{e}^{2x}$。
步骤 9:比较e^x2和${2}^{2x}$的导数
由于e^x2和${2}^{2x}$的导数不相等,所以它们不是同一函数的原函数。
步骤 10:计算x^x的导数
x^x的导数为 $2{x}^{x-1}$。
步骤 11:计算${x}^{2}+{x}^{2}-{x}^{2}$的导数
${x}^{2}+{x}^{2}-{x}^{2}$的导数为 $2{x}^{x-1}$。
步骤 12:比较x^x和${x}^{2}+{x}^{2}-{x}^{2}$的导数
由于x^x和${x}^{2}+{x}^{2}-{x}^{2}$的导数相等,所以它们是同一函数的原函数。
arctanx的导数为 $\dfrac{1}{1+x^2}$。
步骤 2:计算arccotx的导数
arccotx的导数为 $-\dfrac{1}{1+x^2}$。
步骤 3:比较arctanx和arccotx的导数
由于arctanx和arccotx的导数不相等,所以它们不是同一函数的原函数。
步骤 4:计算n5x的导数
n5x的导数为 $\dfrac{1}{5x} \times 5 = \dfrac{1}{x}$。
步骤 5:计算$n5+\ln x$的导数
$n5+\ln x$的导数为 $\dfrac{1}{x}$。
步骤 6:比较n5x和$n5+\ln x$的导数
由于n5x和$n5+\ln x$的导数相等,所以它们是同一函数的原函数。
步骤 7:计算e^x2的导数
e^x2的导数为 $2x{e}^{{x}^{2}}$。
步骤 8:计算${2}^{2x}$的导数
${2}^{2x}$的导数为 $2{e}^{2x}$。
步骤 9:比较e^x2和${2}^{2x}$的导数
由于e^x2和${2}^{2x}$的导数不相等,所以它们不是同一函数的原函数。
步骤 10:计算x^x的导数
x^x的导数为 $2{x}^{x-1}$。
步骤 11:计算${x}^{2}+{x}^{2}-{x}^{2}$的导数
${x}^{2}+{x}^{2}-{x}^{2}$的导数为 $2{x}^{x-1}$。
步骤 12:比较x^x和${x}^{2}+{x}^{2}-{x}^{2}$的导数
由于x^x和${x}^{2}+{x}^{2}-{x}^{2}$的导数相等,所以它们是同一函数的原函数。