__ [例28] (1997,数一)对数螺线 rho =(e)^theta 在点 (rho ,theta )=((e)^n/2,dfrac (pi )(2)) 处的切线的直角坐标方程-|||-[ x+y=(e)^dfrac (x{2)}] -|||-为 __ .
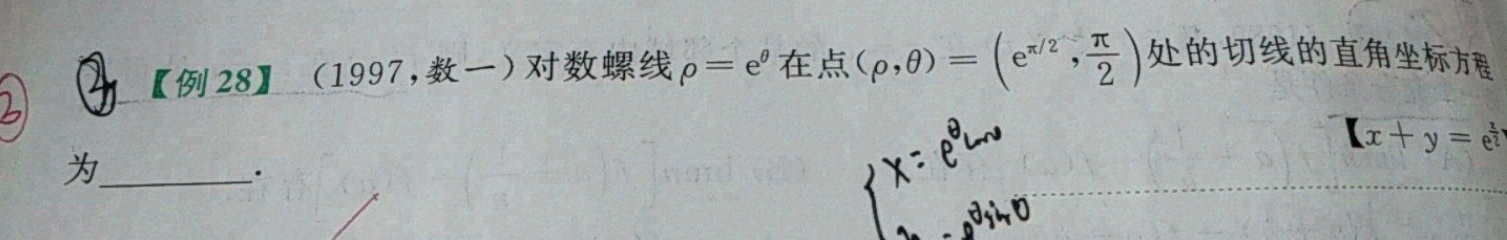
题目解答
答案

解析
考查要点:本题主要考查极坐标方程的切线方程求解,以及极坐标与直角坐标的转换。
解题核心思路:
- 极坐标转直角坐标:利用极坐标与直角坐标的转换公式,确定给定点的直角坐标。
- 求导数得切线斜率:通过极坐标方程求导,得到切线的斜率。
- 写切线方程:结合直角坐标点和斜率,写出切线方程。
破题关键点:
- 极坐标导数公式:正确应用极坐标下切线斜率的公式。
- 代入特定角度:将θ=π/2代入公式,简化计算。
步骤1:确定直角坐标点
极坐标点 $(\rho, \theta) = (e^{\pi/2}, \frac{\pi}{2})$ 转换为直角坐标:
$x = \rho \cos\theta = e^{\pi/2} \cdot \cos\frac{\pi}{2} = 0, \quad y = \rho \sin\theta = e^{\pi/2} \cdot \sin\frac{\pi}{2} = e^{\pi/2}.$
对应直角坐标点为 $(0, e^{\pi/2})$。
步骤2:求切线斜率
极坐标方程 $\rho = e^{\theta}$,导数 $\frac{d\rho}{d\theta} = e^{\theta}$。
切线斜率公式:
$\frac{dy}{dx} = \frac{\frac{d\rho}{d\theta} \sin\theta + \rho \cos\theta}{\frac{d\rho}{d\theta} \cos\theta - \rho \sin\theta}.$
代入 $\rho = e^{\theta}$ 和 $\frac{d\rho}{d\theta} = e^{\theta}$,化简得:
$\frac{dy}{dx} = \frac{e^{\theta} (\sin\theta + \cos\theta)}{e^{\theta} (\cos\theta - \sin\theta)} = \frac{\sin\theta + \cos\theta}{\cos\theta - \sin\theta}.$
当 $\theta = \frac{\pi}{2}$ 时:
$\frac{dy}{dx} = \frac{1 + 0}{0 - 1} = -1.$
步骤3:写切线方程
切线过点 $(0, e^{\pi/2})$,斜率为 $-1$,方程为:
$y - e^{\pi/2} = -1 \cdot (x - 0) \implies x + y = e^{\pi/2}.$