题目
(1)方程 '-y=(e)^x+1 的特解形式可设为-|||-(A) (e)^x+b. (B) (e)^x+b.-|||-(C) (e)^x+bx, (D) (e)^x+bx,

题目解答
答案
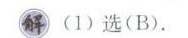
解析
步骤 1:确定齐次方程的解
考虑齐次方程 $y'' - y = 0$,其特征方程为 $r^2 - 1 = 0$,解得 $r = \pm 1$。因此,齐次方程的通解为 $y_h = c_1 e^x + c_2 e^{-x}$。
步骤 2:确定非齐次方程的特解形式
非齐次方程 $y'' - y = e^x + 1$ 的右端项为 $e^x + 1$。由于 $e^x$ 是齐次方程的解,因此特解形式不能直接设为 $a e^x + b$,而应设为 $ax e^x + b$,以避免与齐次方程的解重合。
步骤 3:验证特解形式
将特解形式 $y_p = ax e^x + b$ 代入原方程,验证其是否满足方程。计算 $y_p'$ 和 $y_p''$,并代入原方程,可以验证该形式是正确的。
考虑齐次方程 $y'' - y = 0$,其特征方程为 $r^2 - 1 = 0$,解得 $r = \pm 1$。因此,齐次方程的通解为 $y_h = c_1 e^x + c_2 e^{-x}$。
步骤 2:确定非齐次方程的特解形式
非齐次方程 $y'' - y = e^x + 1$ 的右端项为 $e^x + 1$。由于 $e^x$ 是齐次方程的解,因此特解形式不能直接设为 $a e^x + b$,而应设为 $ax e^x + b$,以避免与齐次方程的解重合。
步骤 3:验证特解形式
将特解形式 $y_p = ax e^x + b$ 代入原方程,验证其是否满足方程。计算 $y_p'$ 和 $y_p''$,并代入原方程,可以验证该形式是正确的。