题目
3.已知当 arrow 0 时, (sqrt (1+a{x)^2}-1) 与sin^2x是等价无穷小,求a的
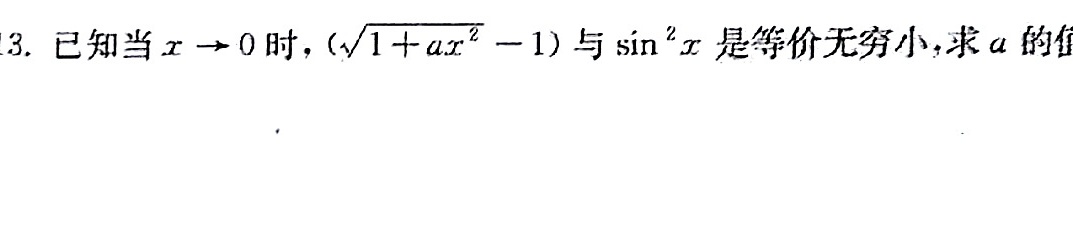
题目解答
答案

解析
考查要点:本题主要考查等价无穷小的定义及泰勒展开的应用,需要学生掌握常见函数的泰勒展开式,并能灵活运用等价无穷小的替换规则。
解题核心思路:
当两个无穷小量 $\alpha(x)$ 和 $\beta(x)$ 满足 $\lim_{x \to 0} \frac{\alpha(x)}{\beta(x)} = 1$ 时,它们互为等价无穷小。本题需将 $\sqrt{1+ax^2} -1$ 和 $\sin^2 x$ 展开至相同阶数,通过比较系数求出 $a$。
破题关键点:
- 泰勒展开:将 $\sqrt{1+ax^2}$ 和 $\sin x$ 展开至二次项,忽略高阶小项。
- 等价替换:利用 $\sqrt{1+t} -1 \approx \frac{t}{2}$(当 $t \to 0$)和 $\sin x \approx x$ 进行简化。
- 极限条件:通过比值极限为1建立方程求解 $a$。
步骤1:展开 $\sqrt{1+ax^2} -1$
当 $x \to 0$ 时,令 $t = ax^2$,则 $\sqrt{1+t} -1$ 的泰勒展开为:
$\sqrt{1+t} -1 = \frac{t}{2} - \frac{t^2}{8} + \cdots$
忽略高阶小项后,近似为:
$\sqrt{1+ax^2} -1 \approx \frac{ax^2}{2}$
步骤2:展开 $\sin^2 x$
利用 $\sin x \approx x - \frac{x^3}{6}$,平方后得:
$\sin^2 x = \left(x - \frac{x^3}{6}\right)^2 = x^2 - \frac{x^4}{3} + \cdots \approx x^2$
步骤3:建立等价无穷小条件
根据题意,$\lim_{x \to 0} \frac{\sqrt{1+ax^2} -1}{\sin^2 x} = 1$,代入近似式:
$\lim_{x \to 0} \frac{\frac{ax^2}{2}}{x^2} = \frac{a}{2} = 1$
解得:
$a = 2$